第 14 章 假设检验的构建
14.1 什么是假设检验
一般来说,我们的假设(或者叫假说) 是对与我们实验观察数据来自的总体(或人群) 的概率分布的描述。在参数检验的背景下,就是要检验描述这个总体(或人群) 的概率分布的参数 (parameters)。最典型的情况是,我们提出两个互补的假设,一个叫作零假设(或者叫原假设) ,null hypothesis (\(H_0\));另一个是与之对应的(互补的) 替代假设,althernative hypothesis (\(H_1/H_A\))。
例如,若 \(X\) 是一个服从二项分布的随机离散变量 \(X\sim Bin(5, \theta)\)。可以考虑如下的零假设和替代假设:\(H_0: \theta=\frac{1}{2}; H_1: \theta=\frac{2}{3}\)。
当建立了零假设和替代假设以后,假设检验就是要建立如下的规则以确定:
- 从样本中计算所得的参数估计值为多少时,拒绝零假设。 (接受替代假设为“真”)
- 从样本中计算所得的参数估计值为多少时,零假设不被拒绝。 (接受零假设为“真”)
注意:(这一段很绕)
上面的例子是零假设和替代假设均为简单假设的情况,实际操作中常常会设计更加复杂的(不对称的) 假设:即简单的 \(H_0\),复杂的 \(H_1\)。如此一来当零假设 \(H_0\) 不被拒绝时,我们并不一定就接受之。因为无证据证明 \(H_1\) 不等于有证据证明 \(H_0\)。 (Absence of evidence is not evidence of absence). 换句话说,无证据让我们拒绝 \(H_0\) 本身并不成为支持 \(H_0\) 为“真”的证据。因为在实际操作中,当我们设定的简单的零假设没有被拒绝,可能还存在其他符合样本数据的零假设;相反地,当样本数据的计算结果拒绝了零假设,我们只能接受替代假设。所以,反对零假设的证据,同时就是支持替代假设的证据。
在样本空间(sample space) 中,决定了零假设 \(H_0\) 会被拒绝的子集( subset),被命名为拒绝域(rejection region ) 或者判别区域(critical region),用 \(\mathfrak{R}\) 来标记。
14.2 错误概率和效能方程
这一部分也可以参考本笔记的临床试验样本量计算 (Section 30 ) 部分。
| \(\underline{x} \notin \mathfrak{R}\) Accept \(H_0\) | \(\underline{x} \in \mathfrak{R}\) Reject \(H_0\) | ||
|---|---|---|---|
| TRUTH | \(H_0\) is true | \(\checkmark\) |
\(\alpha\) Type I error |
| \(H_1\) is true |
\(\beta\) Type II error |
\(\checkmark\) |
假如一个假设检验是关于总体参数 \(\theta\) 的:
\[H_0: \theta=\theta_0 \text{ v.s. } H_1: \theta=\theta_1 \]
这个检验的效能被定义为当替代假设为“真”时,拒绝零假设的概率(该检验方法能够检验出有真实差别的能力) :
\[\text{Power}=\text{Prob}(\underline{x}\in\mathfrak{R}|H_1\text{ is true}) = 1-\text{Prob}(\text{Type II error })\]
观察数据只有两种可能:落在拒绝域内,或者落在拒绝域之外。第二类错误我们常常使用 \(\beta\) 来表示,所以 \(\text{Power}=1-\beta\)。
检验的显著性水平用 \(\alpha\) 来表示。 \(\alpha\) 的直观意义就是,检验结果错误的拒绝了零假设 \(H_0\),接受了替代假设 \(H_1\),即假阳性的概率。
\[\text{Prob}(\underline{x}\in \mathfrak{R} |H_0 \text{ is true})=\text{Prob(Type I error)}\] ### 以二项分布为例
用本文开头的例子: \(X\sim Bin(5,\theta)\)。和我们建立的零假设和替代假设:\(H_0: \theta=\frac{1}{2}; H_1: \theta=\frac{2}{3}\):
考虑两种检验方法:
- A 方法:当且仅当5次观察都为“成功”时才拒绝 \(H_0 (\text{i.e.}\; X=5)\)。所以此时判别区域 \(\mathfrak{R}\) 为 \(5\)。检验效能 \(\text{Power}=1-\beta\) 为:\(Prob(X=5|H_1 \text{ is true})=(\frac{2}{3})^5=0.1317\)。显著性水平 \(\alpha\) 为 \(Prob(X=5|H_0 \text{ is true})=(\frac{1}{2})^5=0.03125\)。
- B 方法:当观察到3,4,5次“成功”时,拒绝 \(H_0 (\text{i.e.} X=3,4,5)\)。此时判别区域 \(\mathfrak{R}\) 为 \(3,4,5\)。检验效能\(Power\) 为:\(Prob(X=3,4,\text{ or }5|H_1 \text{ is ture})=\sum_{i=3}^5(\frac{2}{3} )^i(\frac{1}{3})^{5-i}\approx0.7901\);显著性水平\(\alpha\) 为:\(Prob(X=3,4,5|H_0 \text{ is true})=\sum_{i=3}^5(\frac{1}{2})^i(\frac{1}{2})^{5-i}=0.5\)
## [1] 0.7901235## [1] 0.5比较上面两种检验方法,可以看到,用B方法时,我们有更高的概率获得假阳性结果(犯第一类错误,错误地拒绝\(H_0\),接受\(H_1\)),但是也有更高的检验效能\(1-\beta\)(真阳性更高) 。这个例子就说明了,试图提高检验效能的同时,会提高犯第一类错误的概率。实际操作中我们常常将第一类错误的概率固定,例如 \(\alpha=0.05\),然后尽可能选择检验效能最高的检验方法。
14.3 如何选择要检验的统计量
在上面的二项分布的实验中,“成功的次数” 是我们感兴趣的要检验的统计量。但也可能是第一次出现 “成功” 之前的实验次数,或者,任何与假设相关的统计量。相似的,如果观察不是离散变量而是连续的,可以拿来检验的指标就有很多,如均值,中位数,众数,几何平均值等。
幸运地是,当明确了零假设和替代假设后,我们可以利用Neyman-Pearson lemma 似然比公式1:
来决定使用哪个统计量做检验最有效:
\[\text{Neyman-Pearson lemma}=\frac{L_{H_0}}{L_{H_1}}\]
这公式很直观,因为当观察数据更加支持 \(H_1\) 时 (\(L_{H_1}\) 更大),\(H_0\) 的可能性相对更小,就更应该被拒绝。而且,由于似然比越小,他的对数就越小,实际计算时我们常使用对数似然比:\(\ell_{H_0}-\ell_{H_1}\)。
问题来了,那到底要多小才算小?这个进入拒绝域的阈值由两个指标来决定:
- 被检验统计量的样本分布 (the sampling distribution of the test statistic)
- 第一类错误概率 \(\alpha\) (the required value of \(\alpha\))
14.3.1 以已知方差的正态分布为例
假如已知 \(X_1, \cdots, X_n \stackrel{i.i.d}{\sim} N(\mu, \sigma^2)\) 而且方差 \(\sigma^2\) 也是已知的。如果令\(H_0: \mu=5\; ;H_1: \mu=10\) 可以通过如下的方法找到我们需要的最佳检验统计量best statistic 根据之前的推导(Section @ ref(llr)) 可知正态分布的似然方程如下:
\[\ell(\mu|\underline{x}) =-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2\] 所以已知 \(\sigma^2\) 时,我们的零假设和替代假设之间的对数似然比 \(\ell_{H_0}-\ell_{H_1}\) 为:
\[\ell_{H_0}-\ell_{H_1}=-\frac{1}{2\sigma^2}(\sum_{i=1}^n(x_i-5)^2-\sum_{i= 1}^n(x_i-10)^2)\]
然而,我们只需要考虑随着数据变化的部分,所以忽略掉不变的部分2:
\[ \begin{aligned} \ell_{H_0}-\ell_{H_1} & = -(\sum_{i=1}^n(x_i-5)^2-\sum_{i=i}^n(x_i-10)^2)\ \ & = 75n - 2\times(10-5)\sum_{i=1}^nx_i \\ \end{aligned} \]
所以只要样本和 (sum of sample) \(\sum_{i=1}^nx_i\) (最佳统计量 best statistic) 足够大,零假设就会被拒绝。而且注意到最佳统计量可以乘以任何常数用作新的最佳统计量。为了方便我们就用样本均数 \(\frac{1}{n}\sum_{i=1}^nx_i\) 作此处的最佳统计量。所以此时,我们的最佳检验就是当样本均值足够大,超过某个阈值时,我们拒绝零假设。而且,样本均值的样本分布是可以知道的,这样就便于我们继续计算下一步:拒绝域 (判别区域) 。
14.4 复合假设
目前为止我们讨论的假设检验限制太多,实际操作时,我们多考虑类似如下的假设:
- \(H_0: \theta=\theta_0 \;\text{v.s.}\; H_1: \theta>\theta_0\) [单侧的替代假设]
- \(H_0: \theta=\theta_0 \;\text{v.s.}\; H_1: \theta\neq\theta_0\) [双侧的替代假设]
所以我们面临的问题是简单假设中用于判定的最佳统计量,是始终如一地适用?我们一一来看:
14.5 为反对零假设 \(H_0\) 的证据定量
重新再考虑复合假设:\(H_0: \theta=\theta_0\;\text{v.s.}\;H_1: \theta>\theta_0\) 假如存在一个总是可用的最佳检验统计量,用\(T\) 来标记(或\(T(x)\)), 这个统计量足够大时,我们拒绝\(H_0\)。别忘了我们还要给事先固定好的显著性水平 \(\alpha\) 定义与之相关的判别区域:
\[\text{Prob}(\underline{x}\in\mathfrak{R}|H_0)=\alpha\]
如果我们知道 \(T\) 的样本分布,我们就可以使用一个阈值 \(c\) 来定义这个判别区域:
\[Prob(T\geqslant c|H_0)=\alpha\]
更加正式的,我们定义判别区域 \(\mathfrak{R}\) 为:
\[\{\underline{x}:\text{Prob}(T(x)\geqslant c|H_0)=\alpha\}\]
换句话说,当统计量 \(T>c\) 时,我们拒绝 \(H_0\) 。如果先不考虑拒绝或不拒绝的二元判定,我们可以用一个连续型测量值来量化反对零假设 \(H_0\) 的证据。再考虑从观察数据中获得的 \(T\) ,即数据告诉我们的 \(t\) 。所以,当 \(t\) 值越大,说明观察值相对零假设 \(H_0\) 越往极端的方向走。因此我们可以用 \(T\) 的样本分布来计算观察值大大于等于这个阈值(极端值) 时的概率:
\[p=\text{Prob}(T\geqslant t|H_0)\]
这个概率公式被称为是单侧 \(p\) 值 (one-side p-value)。单侧 \(p\) 值越小,统计量 \(T\) 的样本空间就有越小比例(越强) 的证据支持零假设 \(H_0\)。
我们把这以思想用到假设检验中时,就可以认为:
\[p<\alpha \Leftrightarrow t>c\]
所以用我们一贯的设定 \(\alpha=0.05\),所以如果计算获得 \(p<0.05\) 我们就认为获得了足够强的拒绝零假设 \(H_0\) 的证据。
14.5.1 回到正态分布的均值比较问题上来(单侧替代假设)
继续考虑\(X_1,\cdots,X_n\stackrel{i.i.d}{\sim} N(\mu, \sigma^2)\),假设\(\sigma^2=10\),我们要检验的是\(H_0: \mu =5 \;\text{v.s}.\; H_1: \mu>5\)
- 确定最佳检验统计量:已经证明过,单侧替代假设的最佳检验统计量是样本均值 \(\bar{x}\)。
- 确定该统计量的样本分布:已知样本均数的样本分布是 \(\bar{X}\sim N(\mu,\sigma^2/n)\) 。
\(\Rightarrow Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1)\),所以在\(H_0\) 条件下,\(\ Rightarrow Z=\frac{\bar{X}-5}{\sqrt{10}/\sqrt{n}} \sim N(0,1)\) - 所以当一个检验的显著性水平设定为\(\alpha=0.05\) 时,我们用判别区域\(\mathfrak{R}\),使统计量据落在该判别区域内的概率为\(0.05\):
\(\text{Prob}(\bar{X}\geqslant c|H_0) = 0.05\)
已知在标准正态分布时,\(\text{Prob}(Z\geqslant1.64)=0.05= \text{Prob}(\frac{\bar{X}-5}{\sqrt{10}/\sqrt{n}}\geqslant1.64)\) - 假设样本量是 \(10\),那么数据的判别区域 \(\mathfrak{R}\) 就是 \(\bar{X}\geqslant6.64\)。
- 假设观察数据告诉我们,\(\bar{X}=7.76\) 。那么这一组观察数据计算得到的统计量落在了判别区域内,就提供了足够的证据拒绝接受 \(H_0\)。
- 我们可以给这个观察数据计算相应的单侧\(p\) 值:
\(p=\text{Prob}(\bar{X}\geqslant7.76|H_0)=\text{Prob}(Z +5\geqslant7.76)\\=\text{Prob}(Z\geqslant2.76)=0.003\)
所以,观察数据告诉我们,在\(H_0\) 的前提下,观察值出现的概率是\(0.3 \%\) 。即,在无数次重复取样实验中,仅有 \(0.3\%\) 的结果可以给出支持 \(H_0\) 的证据。因此我们拒绝 \(H_0\) 接受 \(H_1\)。
14.6 双侧替代假设情况下,双侧 \(p\) 值的定量方法
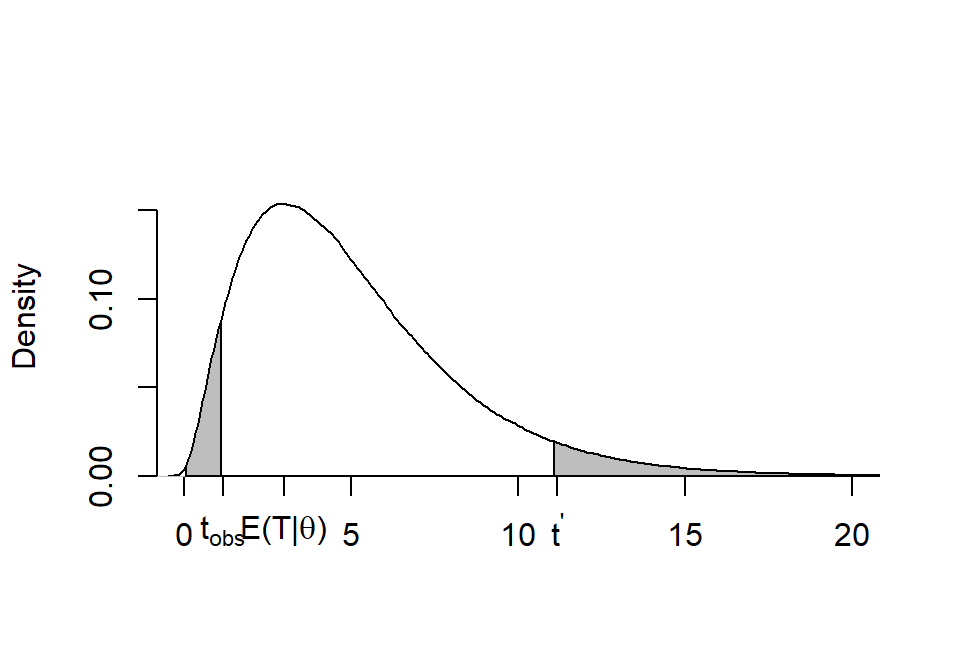
图 14.1: Deliberately use an assymmetrical distribution to highlight the issues
此处故意使用一个左右不对称的概率密度分布来解释。
现在的替代假设是双侧的:
\[H_0: \theta=\theta_0 \;\text{v.s.}\; H_1: \theta\neq\theta_0\]
正常来说,双侧的假设检验应该分成两个单侧检验。即:
- \(H_1: \theta>\theta_0\);
- \(H_1: \theta<\theta_0\).
每个单侧检验都有自己的最佳检验统计量。令 \(T\) 是 1. 的最佳检验统计量,该统计量的样本分布如上图 14.1 所示(左右不对称) 。假如观察数据给出的统计量为 \(t_{\text{obs}}\),那么在概率上反对零假设的情况可以有两种:
- \(T\geqslant t_{\text{obs}}\) 其中, \(\text{Prob}(T\geqslant t_{\text{obs}}|H_0)=\tilde p\);
- \(T\leqslant t^\prime\) 其中,\(t^\prime\) 满足: \(\text{Prob}(T\leqslant t^\prime|H_0) =\tilde p\)。 (图14.1)
所以概率密度分布两侧的距离可以不对称,但是只要左右两侧概率密度分布的面积(\(=\tilde p\))相同,那么就可以直接认为,双侧\(p\) 值是两侧面积之和(\(p=2\times \tilde p\)),且观察数据提供的统计量落在这两个面积内的话,都足以提供证据拒绝零假设\(H_0\)。
注意:
- 被选中的 \(t^\prime\) 值大小不大可能满足:\(|t^\prime - E(T|\theta_0)|=|t_{obs}-E(T|\theta_0)|\)。因为那只有在完全左右对称的分布中才会出现。但是,此处我们关心的是面积左右两边的尾部要相等即可,所以我们只需要知道右半边,较大的那个 \(t_{obs}\) 就完全足够了。
回到上面的均值比较问题 (Section 14.5.1)。现在我们要进行双侧假设检验,即: \(H_0: \mu=5 \text{ v.s. } H_1: \mu\neq5\),最佳统计量依然还是样本均数 \(\bar{X}\)。数据告诉我们说\(\bar{X}=7.76\),因此双侧\(p\) 值就是将已求得的单侧\(\tilde p\) 值乘以\(2\): \(\text{two-sided } p= 2\tilde p= 0.006\)
当然,实际操作中我们很少进行这样繁琐的论证,多数情况下就直接报告双侧 \(p\) 值。
14.7 假设检验构建之总结
按照如下的步骤一一构建我们的假设检验过程:
- 先建立零假设,和替代假设 (Section 14.1);
- 定义最佳检验统计量 (用 Neyman-Pearson lemma) (Section 14.3);
- 取得零假设条件下,最佳统计量的样本分布(通常都较为困难,有时候我们会倾向于使用“不太理想”,但是计算较为简便的过程。) ;
- 定义拒绝域(判别区域) (常用 \(\alpha=0.05\)) ;
- 计算观察数据的检验统计量;
- 如果观察数据的检验统计量落在了提前定义好的拒绝域内,那么我们的检验结论就是:观察数据拒绝了零假设支持替代假设。然而在实际操作时,如果发现数据的检验统计量不在拒绝域内,我们仅仅只能下结论说:观察数据无法拒绝零假设(而不是接受零假设!) ;
- 报告计算得到的反对零假设的定量 \(p\) 值。
作为统计学家,我们的任务是评价数据提供的证据,而不是简单的去接受或者拒绝一个假设。
区分与之前讨论的对数似然比(Section ??),之前讨论的对数似然比指的是所有的似然和极大似然之间的比,此处的似然比只是纯粹在探讨两个假设之间的似然比,与极大似然无关。 ↩︎
Rememer that \(\ell_{H_0}-\ell_{H_1}\) is a random variable: the data varies **each time* * we sample, with consequently varying relative support for the hypotheses, and so we are only interested in that part of \(\ell_{H_0}-\ell_{H_1}\) which depends on the results, the data, which vary with each sample (i.e. which contains the random part); the constant part provides no information on the relative support the data give to the hypotheses, so we ignore it.↩︎