第 31 章 基于秩次的非参数检验
基于秩次的统计学方法不像其他参数检验那样需要太多的假设和前提 (比如服从正态分布或者其它假设)。这类方法其实放弃了数据的部分信息 – 那就是数据之间值的差距。通过给数据排序列,我们仅仅知道数据的排序。所以我们可以下结论说\(A\) 大于\(B\),或者\(B\) 大于\(C\) (因此\(A\) 也大于\(C\)),但是他们之间数值的差距被忽略掉了(所以我们不能比较\(A-B\) 和\(B-C\) 的大小)。
所以,基于秩次的统计学方法完全只依赖数据的大小排序,观察获得数据的真实大小被忽视了。
31.1 符号检验
我们以下列一组空腹血糖测量值的数据为例:
| 10.3 | 8.8 | 5.3 |
| 9.5 | 6.7 | 6.7 |
| 12.2 | 12.5 | 5.2 |
| 15.1 | 4.2 | 13.3 |
| 10.8 | 15.3 | 7.5 |
| 19.0 | 7.2 | 4.9 |
| 16.1 | 9.3 | 19.5 |
| 8.1 | 8.6 | 11.1 |
我们如果想要对这组数据的中位数做出假设检验,\(H_0: \theta = 10; \text{ v.s. } H_1: \theta\neq10\)。
该选择哪种检验方法来回答这个假设检验提出的问题:中位数是否等于 \(10\)?
符号检验 (the sign test),可以用来辅助我们对数据的中位数 (median \(\theta\)) 作出推断 (inference)。虽然往下看你会发现严格说来这并不算是基于秩次的检验方法。使用符号检验时我们需要的唯一假设:数据来自连续分布 (continuous distribution)。
这种类型的检验方法常用的假设检验如下:
\[ H_0: \theta=\theta_0 \\ H_1: \theta\neq\theta_0 \]
其中,\(\theta_0\) 就是我们想要检验的中位数的大小,在上面的例子中,\(\theta_0=10\)。
此时我们用到的检验统计量,\(X\) 的定义是:样本数据中比\(\theta_0\) 大的数据个数,和比\(\theta_0\) 小的数据个数,两个个数中较小的那一个。因为在零假设的条件下,如果观察数据的中位数等于 \(\theta_0\) 的话,数据中比 \(\theta_0\) 大或者小的数据个数应该是相等的。可以用一个二项分布,概率为 \(0.5\) 的模型来模拟:
\[X\sim Bin(n, 0.5)\]
在本例中,观察数据有 13 个小于 \(\theta_0=10\),有 11 个大于 \(\theta_0=10\)。因此 \(X=11, n=24\)。假如 \(\pi\) 是一个观察数据大于 \(\theta_0\) 的概率的话,在零假设的条件下,\(H_0: \pi=0.5\)。检验这个假设的双侧概率的计算公式为:
\[2\times P(X\leqslant x|\pi=0.5)\]
在本例中, \(X=11\)。如果(像在考试的时候没有电脑辅助)要用查表的方式判断 \(p\) 值大小。
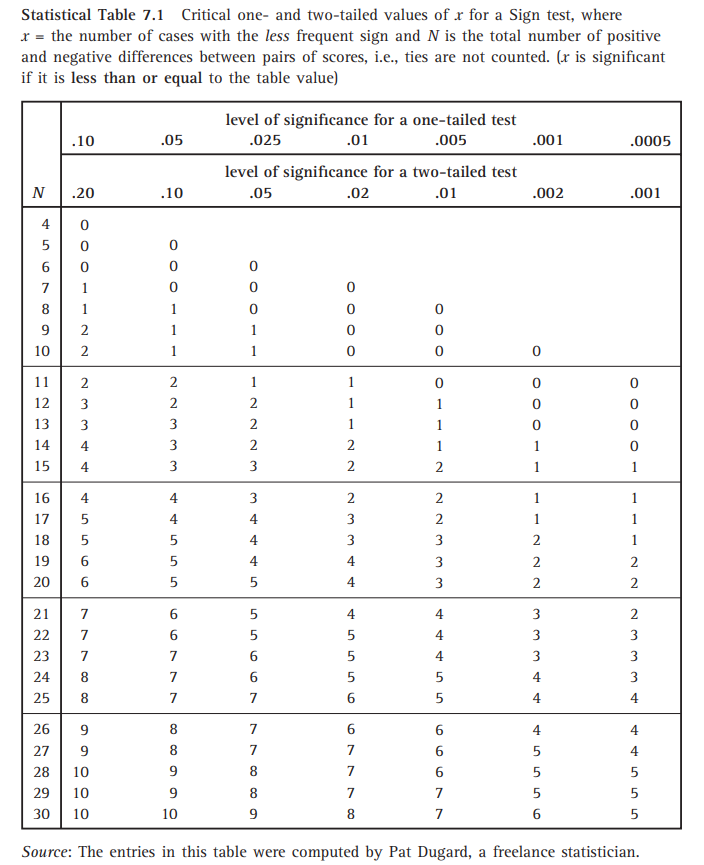
\[\cdots\cdots\cdots\]
找到 \(n=24\) 这一行,发现显著性水平是 \(20\%\) 的拒绝域都要小于 \(8\), 所以本例的 \(p>20\%\)。
现在可以直接用R之后计算:
## [1] 0.8388197或者可以使用命令 binom.test 来做一个二项分布的概率检验:
options(scipen = 1, digits = 8) # just to show the p values are exactly the same
binom.test(11,24,0.5)##
## Exact binomial test
##
## data: 11 and 24
## number of successes = 11, number of trials = 24, p-value = 0.83882
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.25553020 0.67179192
## sample estimates:
## probability of success
## 0.45833333或者你也可以使用 BSDA 中的 SIGN.test 命令来进行的符号检验:
options(scipen = 1, digits = 8)
# input the data
dt <- c(10.3,9.5,12.2,15.1,10.8,19.0,16.1, 8.1, 8.8, 6.7,12.5, 4.2,15.3, 7.2, 9.3, 8.6, 5.3,6.7 ,5.2,13.3, 7.5, 4.9,19.5,11.1)
BSDA::SIGN.test(dt, md=10, alternative="two.sided", conf.level=0.95)##
## One-sample Sign-Test
##
## data: dt
## s = 11, p-value = 0.83882
## alternative hypothesis: true median is not equal to 10
## 95 percent confidence interval:
## 7.3988241 12.3011759
## sample estimates:
## median of x
## 9.4
##
## Achieved and Interpolated Confidence Intervals:
##
## Conf.Level L.E.pt U.E.pt
## Lower Achieved CI 0.9361 7.5000 12.2000
## Interpolated CI 0.9500 7.3988 12.3012
## Upper Achieved CI 0.9773 7.2000 12.5000总而言之无论你用的是哪个方法,结果都是一样的:数据无法提供足够的证据拒绝零假设,即无证据证明中位数不等于10。
需要注意的是,如果观察数据中有的值恰好等于 \(\theta_0\) 那么这些观察数据就会被剔除之后再进行检验,相应的样本量 (\(n\)) 也就变小了。如果观察数据样本量足够大,我们可以使用二项分布的正态分布近似 (Section 8.4) 法计算。近似法计算时记得要进行校正 (Section 8.6):
\[ z=\frac{\frac{x}{n}-\pi}{\sqrt{\pi(1-\pi)/n}}=\frac{\frac{x}{n}-0.5}{\ sqrt{0.5(1-0.5)/n}}=\frac{2x}{\sqrt{n}}-\sqrt{n}\\ \text{With the continuity correction, this becomes: }\\ z=\lvert\frac{2x}{\sqrt{n}}-\sqrt{n}\rvert-\frac{1}{\sqrt{n}} \]
在本例中:
\[z=\lvert\frac{2\times11}{\sqrt{24}}-\sqrt{24}\rvert-\frac{1}{\sqrt{24}}=0.204\]
标准正态分布的 \(z\) 为 \(0.204\) 时的双侧 \(p\) 值为:
## [1] 0.8383535和前面的直接计算法的结果还算是十分接近的。
31.2 Wilcoxon 符号秩和检验
Wilcoxon 符号秩和检验也可以用来检验一组数据的中位数是否和某个已知数字相等。进行本方法时除了像符号检验那样要假设数据是连续的以外,还要假设数据的分布是左右对称的。因此,由于假定了左右对称的前提,中位数也就等于均数,所以它也可以被用于检验均数是否等于某个已知的值。
Wilcoxon 符号秩和检验的前提可以被认为是介于符号检验和单一样本 \(t\) 检验 (还假设数据来自于正态分布) 之间的一种检验。
当一组随机观察数据 \(x_1,\cdots,x_n\) 来自于对称的连续分布数据。如果它的中位数是 \(\theta\),在零假设:\(H_0: \theta=\theta_0\) 的条件下:
- 将全部观察数据一一和 \(\theta_0\) 相减,那么每一个 \(d_i=x_i-\theta_0, i=1,2,\cdots,n\) 的正负符号概率是相等的;
- 任何一个和 \(\theta_0\) 相减之后的差 \(\lvert d_i \lvert\) ,取正负符号的概率是相等的。
这里我们使用另一个例子来说明 Wilcoxon 检验法。下列数据为,12名女性从平躺姿势改成直立时心跳次数的变化 (次/分)。
-2, -5, 12, 4, 16, 17, 8, 3, 20, 25, 1, 9
下面来使用 Wilcoxon 符号秩和检验法来检验中位数 \(\theta=15\)。
首先,先计算每个数据和 \(15\) 之间的差值:
## [1] -17 -20 -3 -11 1 2 -7 -12 5 10 -14 -6下一步,计算这些差值的绝对值:
## [1] 17 20 3 11 1 2 7 12 5 10 14 6Dt <- data.frame(data, newdata, abs_newdata)
Dt <- Dt[order(newdata), ] # sort the data by newdata
Dt## data newdata abs_newdata
## 2 -5 -20 20
## 1 -2 -17 17
## 11 1 -14 14
## 8 3 -12 12
## 4 4 -11 11
## 7 8 -7 7
## 12 9 -6 6
## 3 12 -3 3
## 5 16 1 1
## 6 17 2 2
## 9 20 5 5
## 10 25 10 10之后,给绝对值排序:
## data newdata abs_newdata ranks
## 2 -5 -20 20 12
## 1 -2 -17 17 11
## 11 1 -14 14 10
## 8 3 -12 12 9
## 4 4 -11 11 8
## 7 8 -7 7 6
## 12 9 -6 6 5
## 3 12 -3 3 3
## 5 16 1 1 1
## 6 17 2 2 2
## 9 20 5 5 4
## 10 25 10 10 7接下来,给小于 \(15\) 的数据的排序加上负号:
## data newdata abs_newdata ranks signed_ranks
## 5 16 1 1 1 1
## 6 17 2 2 2 2
## 3 12 -3 3 3 -3
## 9 20 5 5 4 4
## 12 9 -6 6 5 -5
## 7 8 -7 7 6 -6
## 10 25 10 10 7 7
## 4 4 -11 11 8 -8
## 8 3 -12 12 9 -9
## 11 1 -14 14 10 -10
## 1 -2 -17 17 11 -11
## 2 -5 -20 20 12 -12对正的负的 signed_ranks 分别求和,绝对值较小的那个就是 Wilcoxon 检验的统计量。本例中:\(S^+=\) 14,\(S^-=\) -64,所以本例中的检验统计量等于\(14\)。如果要继续查表的话,可以找到 \(0.05<p<0.1\):
 \[\cdots\cdots\cdots\]
\[\cdots\cdots\cdots\]

图 31.1: Critical Values for a Wilcoxon Signed-Ranks test
精确的 Wilcoxon 符号秩和检验可以通过下列代码在R里完成:
##
## Wilcoxon signed rank exact test
##
## data: Dt$data
## V = 14, p-value = 0.052246
## alternative hypothesis: true location is not equal to 15如果数据中有观察值和我们希望比较的数值完全相等的话,和符号检验类似的,这些观察值需要被剔除之后再进行上面的个步骤检验。记得还要将样本量减去相应个数再去查表寻找 \(p\) 值。
另外,下面的代码可以计算正态分布近似的 Wilcoxon 秩和检验,结果十分接近:
##
## Wilcoxon signed rank test
##
## data: Dt$data
## V = 14, p-value = 0.04986
## alternative hypothesis: true location is not equal to 15值得注意的是,精确计算时,我们需要剔除那些和比较数值完全一致的观察值。然而在正态分布近似法的 Wilcoxon 检验中,这些数值并不会被剔除,而是保留下来,并且用于对方差进行调整。 Wilcoxon 秩和检验可以在我们能够假设数据左右对称分布,且明显不服从正态分布时使用 (即概率密度分布图左右两端的尾部较厚的时候)。如果数据左右完全对称,本检验方法不太推荐采用。
31.3 Wilcoxon-Mann-Whitney (WMW) 检验
本方法用于比较两组独立样本的分布是否只是左右位移 (或者叫平移)。此检验需要的假设前提为:两组独立样本来自连续型分布,且仅仅只存在整体的左右位移 (或者叫平移) (location shift)。
例如说,两组数据各自的累积概率方程分别是 \(F(\cdot), G(\cdot)\) 时,由上面的假设可知:
\[G(y)=F(y-\Delta), \text{ where } -\infty<\Delta<\infty\]
上面式子中的 \(\Delta\) 就是所谓的 “左右位移 (或者叫平移)”。因此本检验的零假设和替代假设为:
\[H_0: \Delta=0\\ H_1: \Delta\neq0\]
在零假设的条件下,我们可以认为两个样本来自相同的人群分布。假如,\(F, G\) 都是正态分布,且同方差。那么 \(\Delta\) 就等于两个分布的均值差。在这种情况下就可以使用两样本 \(t\) 检验。所以说,WMW 检验其实就是把假设前提放宽了的 (免去了正态分布假设) 两样本 \(t\) 检验。
如果两个独立样本分别有样本量 \(n, m, \text{ and } n<m\):\(X_1,\cdots,X_n\) 和 \(Y_1, \cdots, Y_m\)。在零假设的条件下,将这两个样本合并之后的大样本 (\(m+n\) 个样本量) :\(X_1,\cdots,X_n,Y_1, \cdots, Y_m\) 可以视为来自同一分布。那么在合并后的样本中,我们给每一个元素赋予它们的合并后数据中的排序(\(\text{Rank}_i: i= 1,2,\cdots,n, n+1, \cdots, n +m\))。那么我们感兴趣的 Wilcoxon 秩和统计量 (Wilcoxon rank sum statistic) \(W_1\) 是样本量较小的那些数字在合并后数据中的排序之和。
\[W_1=\sum_{i=1}^n R_i\]
对于大小相同的数据,排序取他们的排序的平均值。
之后再计算 :
\[U_1=W_1+\frac{n(n+1)}{2}\]
最后拿来判断的检验统计量是 \(U_1\) 和 \(n\times m -U_1\) 两者中较小的数字。 (注:如果我们一开始计算样本量较多的部分的秩和\(W_2=\sum_{i=1}^m R_i\) 时,将计算的\(U_2=W_2-\frac{m(m+1) }{2}\),跟\(n\times m - U_2\) 中较小的数字作为检验统计量的话,我们会在数学上获得完全一样的检验统计量。)
其实两个统计量 \(W, U\) 均可以用来作相同的统计推断,当然各自的 \(p\) 值表格不同。但是 \(U\) 有另外一种统计学含义:\(U\) 是 \(X_i>Y_j\), 也就是所有的 \((X_i, Y_j)\) 配对中 \(X_i\) 较大的对的个数。
这里使用下面的例子来解释如何操作 WMW 检验: 采集16名甲亢儿童的血清甲状腺素浓度值列表如下,
| thyr | group |
|---|---|
| 34 | Slight or no symptoms |
| 45 | Slight or no symptoms |
| 49 | Slight or no symptoms |
| 55 | Slight or no symptoms |
| 58 | Slight or no symptoms |
| 59 | Slight or no symptoms |
| 60 | Slight or no symptoms |
| 62 | Slight or no symptoms |
| 86 | Slight or no symptoms |
| 5 | Marked symptoms |
| 8 | Marked symptoms |
| 18 | Marked symptoms |
| 24 | Marked symptoms |
| 60 | Marked symptoms |
| 84 | Marked symptoms |
| 96 | Marked symptoms |
这里我们需要比较轻微症状组和严重症状组的血清甲状腺浓度的分布是否只是左右位移,\(H_0: \Delta=0\)。
首先,我们要给两组合并后的浓度排序:
## thyr group rank
## 10 5 Marked symptoms 1.0
## 11 8 Marked symptoms 2.0
## 12 18 Marked symptoms 3.0
## 13 24 Marked symptoms 4.0
## 1 34 Slight or no symptoms 5.0
## 2 45 Slight or no symptoms 6.0
## 3 49 Slight or no symptoms 7.0
## 4 55 Slight or no symptoms 8.0
## 5 58 Slight or no symptoms 9.0
## 6 59 Slight or no symptoms 10.0
## 7 60 Slight or no symptoms 11.5
## 14 60 Marked symptoms 11.5
## 8 62 Slight or no symptoms 13.0
## 15 84 Marked symptoms 14.0
## 9 86 Slight or no symptoms 15.0
## 16 96 Marked symptoms 16.0Wilcoxon 统计量 \(W_1\) 是人数少的组的排序之数值和。本样本中 7 人有严重症状,9人有轻微或无症状。所以 \(W_1\) 就是严重症状组的秩和:
\[W_1=1+2+3+4+11.5+14+16=51.5\]
再计算统计量 \(U_1\):
\[U_1=W_1-\frac{n(n+1)}{2}=51.5-\frac{7\times(7+1)}{2}=23.5\]
所以 \(n\times m-U_1=7\times9-23.5=39.5\),显然这两个数值中小的 \(23.5\) 就是我们寻找的 WMW 统计量。继续查表:
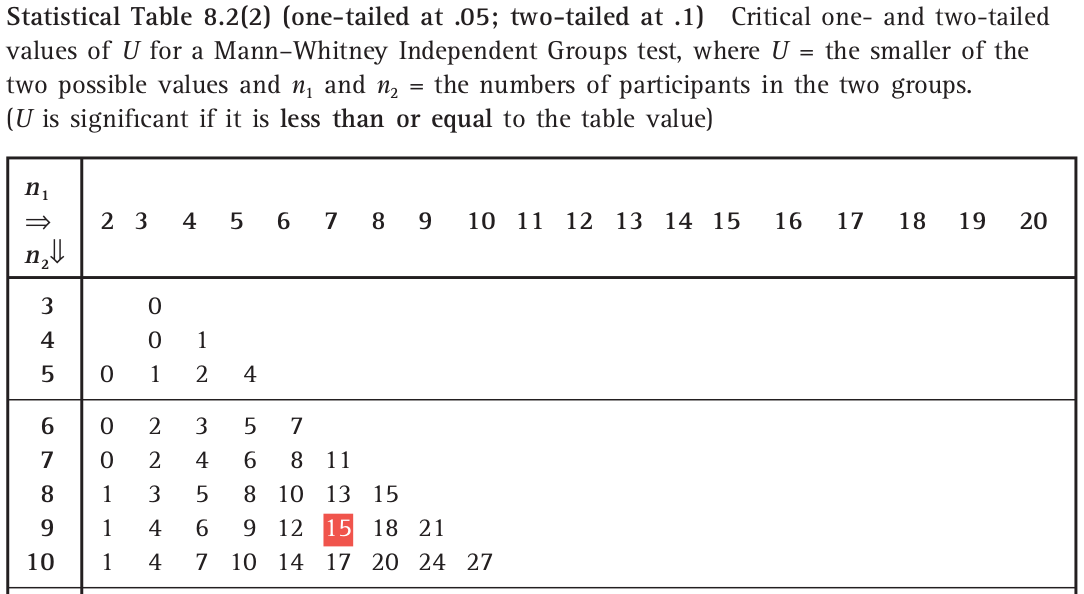
图 31.2: Critical Values of U for a Wilcoxon-Mann-Whitney test
可知 \(n_1=7, n_2=9\) 时,统计量要低于 \(15\) \(p\) 值才会小于 \(0.1\)。所以数据给出的 \(p>0.1\)。
在 R 里面用下面的代码进行 WHW 检验:
##
## Wilcoxon rank sum test
##
## data: dt$thyr by dt$group
## W = 23.5, p-value = 0.39675
## alternative hypothesis: true location shift is not equal to 0##
## Wilcoxon rank sum test with continuity correction
##
## data: dt$thyr by dt$group
## W = 23.5, p-value = 0.42692
## alternative hypothesis: true location shift is not equal to 031.4 秩相关
Spearman 的秩相关 (通常用 \(\rho\)),是一种基于数据排序的相关系数算法。和传统的 Pearson 相关系数类比,是当数据无法被认定是线性相关时的另一种相关关系检验方法。所以秩相关不假定两组数据之间是线性相关 (linear association)。秩相关只关心一个数据递增时,另一个数据是否单调递增。所以可以用于倾向性检验。
具体的操作是,在两组数据中先各自排序,像所有的排序检验一样遇到相同大小的数值将排序取均值。之后使用一般的求相关系数的方法。本法中只用到了数值在各自组中的排序,并没有使用他们的真实大小。近似法的秩相关计算公式为:
\[\hat\tau=\frac{\hat\rho}{\sqrt{(1-\hat\rho^2)/(n-2)}}\]
在零假设条件下 \(H_0: \rho=0\),上面的近似法秩相关服从 \(t_{n-2}\) 分布。 下面用某血友病患者调查数据获得的血液 \(T_4, T_8\) 淋巴球计数 \((\times10^9/\ell)\) 来详细解释计算过程:
| th4 | th8 |
|---|---|
| 0.20 | 0.17 |
| 0.27 | 0.52 |
| 0.28 | 0.25 |
| 0.37 | 0.34 |
| 0.38 | 0.14 |
| 0.48 | 0.10 |
| 0.49 | 0.58 |
| 0.56 | 0.23 |
| 0.60 | 0.24 |
| 0.64 | 0.67 |
| 0.64 | 0.90 |
| 0.66 | 0.26 |
| 0.70 | 0.61 |
| 0.77 | 0.18 |
| 0.88 | 0.74 |
| 0.88 | 0.54 |
| 0.88 | 0.76 |
| 0.90 | 0.62 |
| 1.02 | 0.48 |
| 1.10 | 0.58 |
| 1.10 | 0.34 |
| 1.18 | 0.84 |
| 1.20 | 0.63 |
| 1.30 | 0.46 |
| 1.40 | 0.84 |
| 1.60 | 1.20 |
| 1.64 | 0.59 |
| 2.40 | 1.30 |
给这组数据绘制散点图:
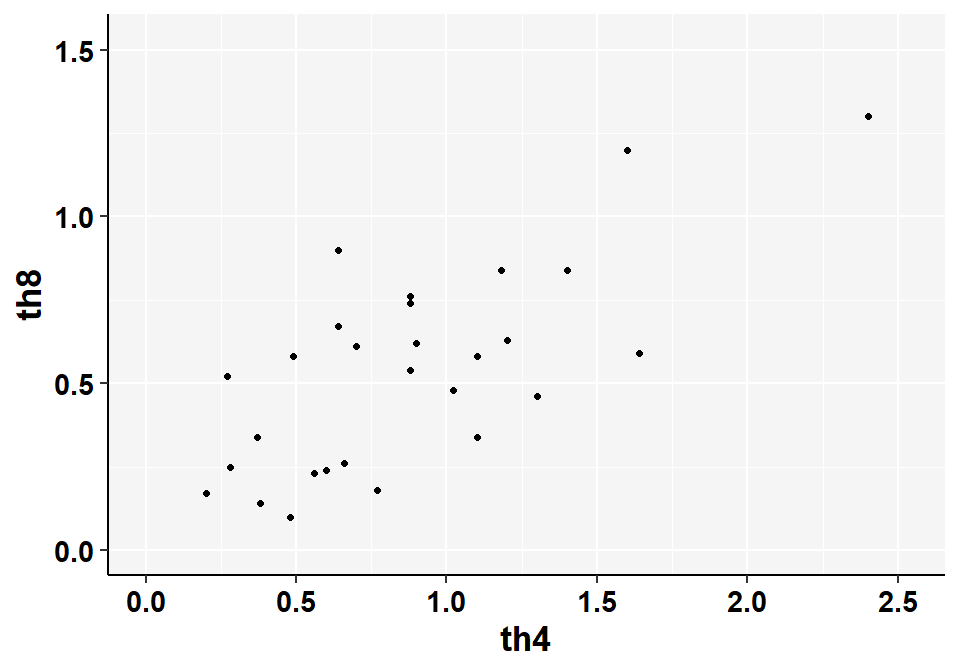
图 31.3: Scatter plot of T4 and T8 counts
可以看见图中右上角的两个点几乎可以认为是异常值 (outliers)。
分别给 th4, th8 求各自的排序:
dt$rank4 <- rank(dt$th4)
dt$rank8 <- rank(dt$th8)
kable(dt, "html", align = "c",caption = "Lymphocyte counts") %>%
kable_styling(bootstrap_options = c("striped", "bordered")) %>%
# collapse_rows(columns = c(1)) %>%
add_header_above(c("n=28 haemophiliacs with ranks" = 4)) %>%
scroll_box(width = "400px", height = "500px", extra_css="margin-left: auto; margin-right: auto;")| th4 | th8 | rank4 | rank8 |
|---|---|---|---|
| 0.20 | 0.17 | 1.0 | 3.0 |
| 0.27 | 0.52 | 2.0 | 13.0 |
| 0.28 | 0.25 | 3.0 | 7.0 |
| 0.37 | 0.34 | 4.0 | 9.5 |
| 0.38 | 0.14 | 5.0 | 2.0 |
| 0.48 | 0.10 | 6.0 | 1.0 |
| 0.49 | 0.58 | 7.0 | 15.5 |
| 0.56 | 0.23 | 8.0 | 5.0 |
| 0.60 | 0.24 | 9.0 | 6.0 |
| 0.64 | 0.67 | 10.5 | 21.0 |
| 0.64 | 0.90 | 10.5 | 26.0 |
| 0.66 | 0.26 | 12.0 | 8.0 |
| 0.70 | 0.61 | 13.0 | 18.0 |
| 0.77 | 0.18 | 14.0 | 4.0 |
| 0.88 | 0.74 | 16.0 | 22.0 |
| 0.88 | 0.54 | 16.0 | 14.0 |
| 0.88 | 0.76 | 16.0 | 23.0 |
| 0.90 | 0.62 | 18.0 | 19.0 |
| 1.02 | 0.48 | 19.0 | 12.0 |
| 1.10 | 0.58 | 20.5 | 15.5 |
| 1.10 | 0.34 | 20.5 | 9.5 |
| 1.18 | 0.84 | 22.0 | 24.5 |
| 1.20 | 0.63 | 23.0 | 20.0 |
| 1.30 | 0.46 | 24.0 | 11.0 |
| 1.40 | 0.84 | 25.0 | 24.5 |
| 1.60 | 1.20 | 26.0 | 27.0 |
| 1.64 | 0.59 | 27.0 | 17.0 |
| 2.40 | 1.30 | 28.0 | 28.0 |
接下来再给 th4, th8 的排序做散点图:
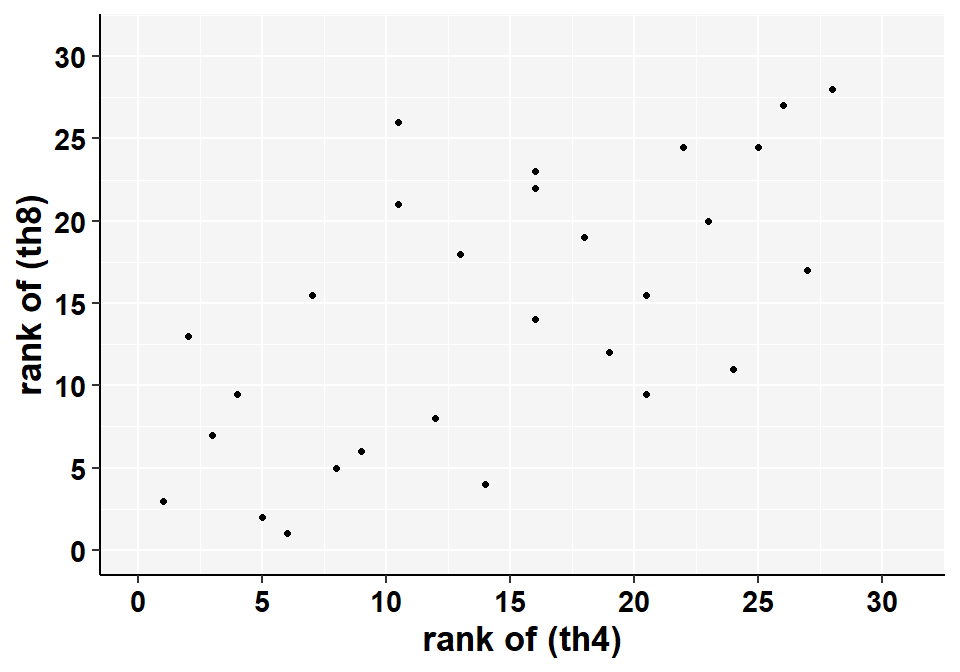
图 31.4: Scatter plot of T4 and T8 ranks
此时也就没有了异常值的存在。对二者的排序计算相关系数:
##
## Pearson's product-moment correlation
##
## data: dt$rank4 and dt$rank8
## t = 4.11513, df = 26, p-value = 0.00034606
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.33297073 0.81107104
## sample estimates:
## cor
## 0.62803129##
## Pearson's product-moment correlation
##
## data: dt$th4 and dt$th8
## t = 5.28031, df = 26, p-value = 0.000016061
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.47328797 0.86128090
## sample estimates:
## cor
## 0.71934766秩相关的相关系数为 \(0.628\)。而原始数据的相关系数为 \(0.719\)。