第 12 章 似然
12.1 概率 vs. 推断
在概率论的环境下,我们常常被告知的前提是:某某事件发生的概率是多少。例如: 一枚硬币正面朝上的概率是 \(0.5\; Prob(coin\;landing\;heads)=0.5\)。然后在这个前提下,我们又继续去计算复杂的事件发生的概率(例如,10次投掷硬币以后4次正面朝上的概率是多少?) 。
\[ \binom{10}{4}\times(0.5^4)\times(0.5^{10-4}) = 0.205 \]
## [1] 0.2050781## [1] 0.2050781在统计推断的理论中,我们考虑实际的情况,这样的实际情况就是,我们通过观察获得数据,然而我们并不知道某事件发生的概率到底是多少(神如果存在话,只有神知道) 。故这个 \(Prob(coin\;landing\;heads)\) 的概率大小对于“人类”来说是未知的。我们可能观察到投掷了10次硬币,其中有4次是正面朝上的。那么我们从这一次观察实验中,需要计算的是能够符合观察结果的“最佳”概率估计 (best estimate)。在这种情况下,似然法 (likelihood) 就是我们进行参数估计的最佳手段。
12.2 似然和极大似然估计
此处用二项分布的例子来理解似然法的概念:假设我们观察到10个对象中有4个患中二病,我们假定这个患病的概率为 \(\pi\)。于是我们就有了下面的模型:
模型: 我们假定患病与否是一个服从二项分布的随机变量,\(X\sim Bin(10,\pi)\)。同时也默认每个人之间是否患病是相互独立的。
数据: 观察到的数据是,10人中有4人患病。于是 \(x=4\)。
现在按照观察到的数据,参数 \(\pi\) 变成了未知数:
\[Prob(X=4|\pi)=\binom{10}{4}\pi^4(1-\pi)^{10-4}\]
此时我们会很自然的考虑,当 \(\pi\) 是未知数的时候,它取值为多大的时候才能让这个事件(即:10人中4人患病) 发生的概率最大? 所以我们可以将不同的数值代入 \(\pi\) 来计算该事件在不同概率的情况下发生的可能性到底是多少:
| \(\pi\) | 事件 \(X=4\) 发生的概率 |
|---|---|
| 0.0 | 0.000 |
| 0.2 | 0.088 |
| 0.4 | 0.251 |
| 0.5 | 0.205 |
| 0.6 | 0.111 |
| 0.8 | 0.006 |
| 1.0 | 0.000 |
很显然,如果 \(\pi=0.4\) 时,我们观察到的事件发生的概率要比 \(\pi\) 取其它值时更大。于是小总结一下目前为止的步骤如下:
- 观察到实验数据(10人中4个患病) ;
- 假定这数据服从二项分布的概率模型,计算不同(\(\pi\) 的取值不同的) 情况下,该事件按照假定模型发生的概率;
- 通过比较,我们选择了能够让观察事件发生概率最高的参数取值 (\(\pi=0.4\))。
至此,我们可以知道,似然方程,是一个关于未知参数\(\pi\) 的函数,我们目前位置做的就是找到这个函数的最大值(maximised),和使之成为最大值时的\(\pi\) :
\[L(\pi|X=4)=\binom{10}{4}\pi^4(1-\pi)^{10-4}\]
我们可以画出这个似然方程的图形, \(\pi\in[0,1]\)
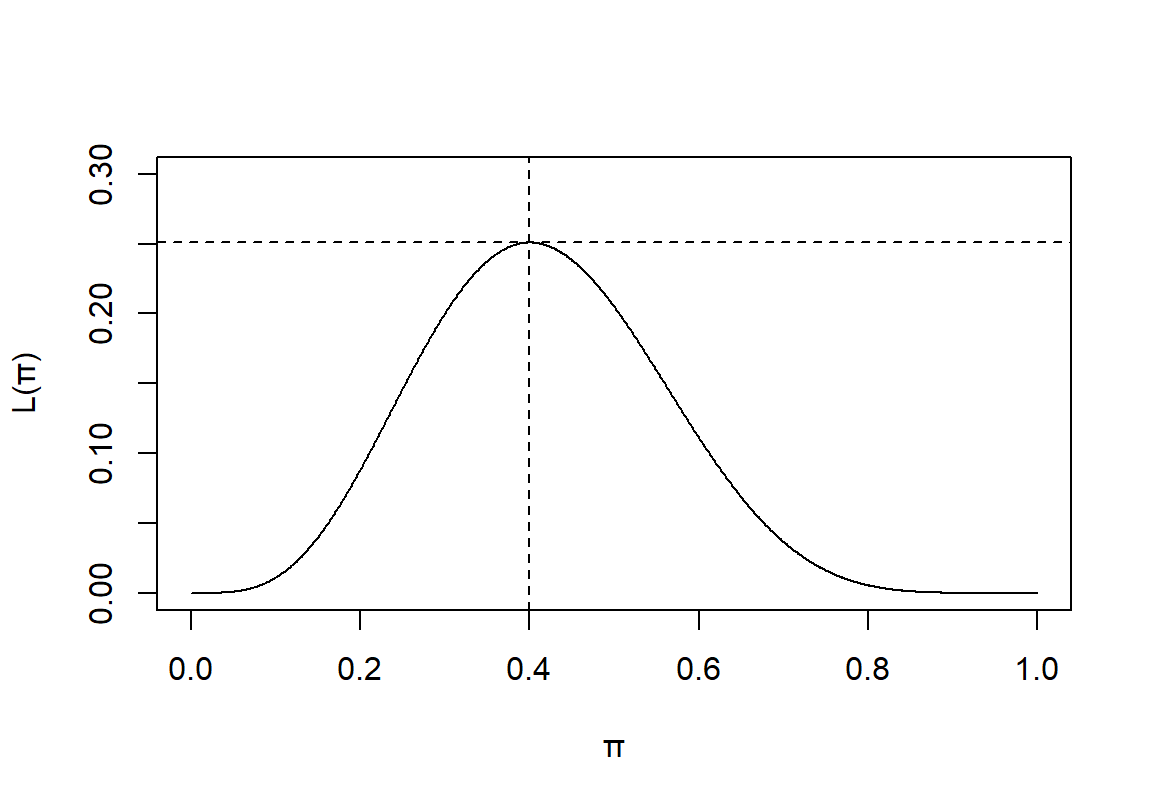
图 12.1: Binomial Likelihood
从图形上我们也能确认,\(\pi=0.4\) 时能够让这个似然方程取得最大值。
12.3 似然方程的一般化定义
对于一个概率模型,如果其参数为 \(\theta\),那么在给定观察数据 \(\underline{x}\) 时,该参数的似然方程被定义为:
\(L(\theta|\underline{x})=P(\underline{x}|\theta)\)
注意:
- \(P(\underline{x}|\theta)\) 可以是概率(离散分布) 方程,也可以是概率密度(连续型变量) 方程。对于此方程,\(\theta\) 是给定的,然后再计算某些事件发生的概率。
- \(L(\theta|\underline{x})\) 是一个关于参数 \(\theta\) 的方程,此时,\(\underline{x}\) 是固定不变的(观察值) 。我们希望通过这个方程求出能够使观察到的事件发生概率最大的参数值。
- 似然方程不是一个概率密度方程。
另一个例子:
有一组观察数据是离散型随机变量 \(X\),它符合概率方程 \(f(x|\theta)\)。下表罗列了当\(\theta\) 分别取值\(1,2,3\) 时的概率方程的值,试求每个观察值\(X = 0,1,2,3,4\) 的最大似然参数估计:
| \(x\) | \(f(x|1)\) | \(f(x|2)\) | \(f(x|3)\) |
|---|---|---|---|
| 0 | 1/3 | 1/4 | 0 |
| 1 | 1/3 | 1/4 | 0 |
| 2 | 0 | 1/4 | 1/6 |
| 3 | 1/6 | 1/4 | 1/2 |
| 4 | 1/6 | 0 | 1/3 |
| \(x\) | \(f(x|1)\) | \(f(x|2)\) | \(f(x|3)\) | \(\theta\) |
|---|---|---|---|---|
| 0 | 1/3 | 1/4 | 0 | 1 |
| 1 | 1/3 | 1/4 | 0 | 1 |
| 2 | 0 | 1/4 | 1/6 | 2 |
| 3 | 1/6 | 1/4 | 1/2 | 3 |
| 4 | 1/6 | 0 | 1/3 | 3 |
12.4 对数似然方程
似然方程的最大值,可通过求 \(L(\theta|data)\) 的最大值获得,也可以通过求该方程的对数方程 \(\ell(\theta|data)\) 的最大值获得。传统上,我们估计最大方程的最大值的时候,会给参数戴一顶“帽子”(因为这是观察获得的数据告诉我们的参数) : \(\hat{\theta}\)。并且我们发现对数似然方程比一般的似然方程更加容易微分,因此求似然方程的最大值就变成了求对数似然方程的最大值:
\[\frac{d\ell}{d\theta}=\ell^\prime(\theta)=0\\ AND\\ \frac{d^2\ell}{d\theta^2}<0\]
要注意的是,微分不一定总是能帮助我们求得似然方程的最大值。如果说参数本身的定义域是有界限的话,微分就行不通了:
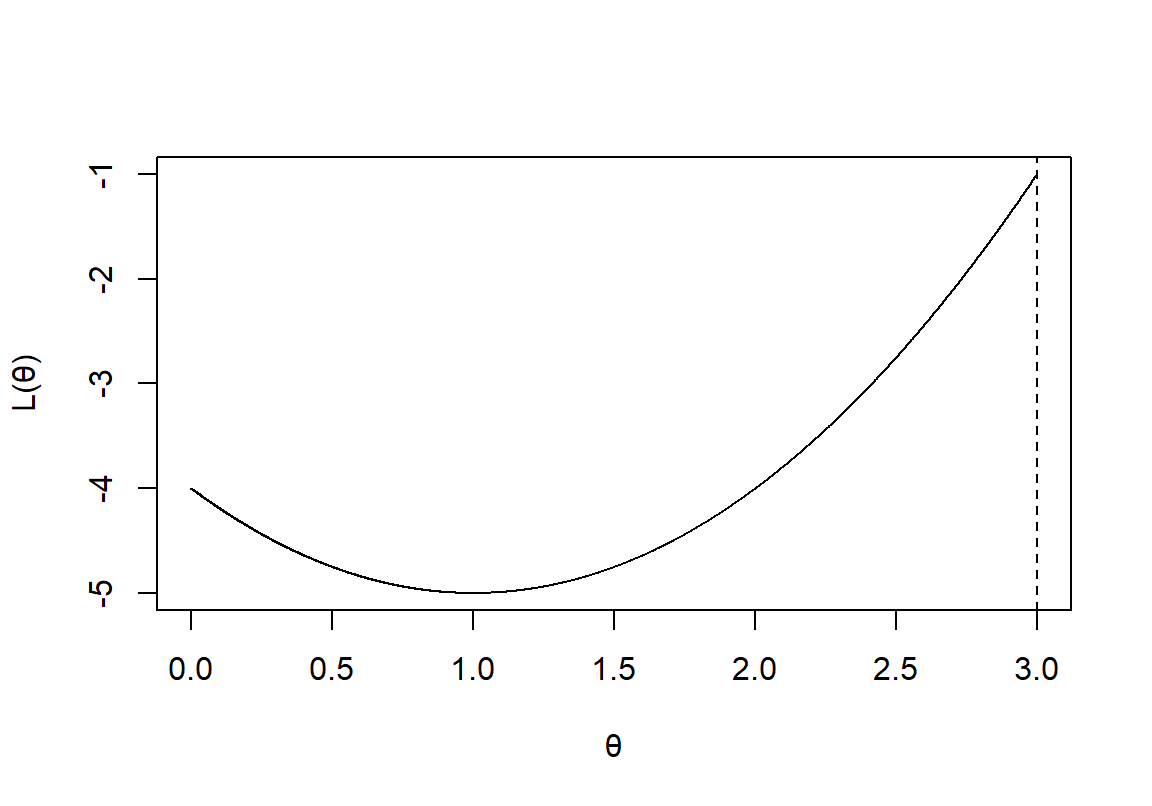
图 12.2: Likelihood function with a limited domain
证明:当 \(L(\theta|data)\) 取最大值时,该方程的对数方程 \(\ell(\theta|data)\) 也是最大值:
如果似然方程是连续可导,只有一个最大值,且可以二次求导,假设 \(\hat{\theta}\) 使该方程取最大值,那么:
\[\frac{dL}{d\theta}=0, \frac{d^2L}{d\theta^2}<0 \Rightarrow \theta=\hat{\theta}\] 令 \(\ell=\text{log}L\) 那么 \(\frac{d\ell}{dL}=\ell^\prime=\frac{1}{L}\):
\[\frac{d\ell}{d\theta}=\frac{d\ell}{dL}\cdot\frac{dL}{d\theta}=\frac{1}{L}\cdot\frac{dL}{d\theta}\]
当 \(\ell(\theta|data)\) 取最大值时:
\[\frac{d\ell}{d\theta}=0\Leftrightarrow\frac{1}{L}\cdot\frac{dL}{d\theta}=0\\ \because \frac{1}{L}\neq0 \\ \therefore \frac{dL}{d\theta}=0\\ \Leftrightarrow \theta=\hat{\theta}\]
\[ \begin{aligned} \frac{d^2\ell}{d\theta^2} &= \frac{d}{d\theta}(\frac{d\ell}{dL}\cdot\frac{dL}{d\theta})\\ &= \frac{d\ell}{dL}\cdot\frac{d^2L}{d\theta^2} + \frac{dL}{d\theta}\cdot\frac{d}{d\theta}(\frac{d\ell}{dL}) \end{aligned} \]
当\(\theta=\hat{\theta}\) 时,\(\frac{dL}{d\theta}=0\) 且\(\frac{d^2L}{d\theta^2}<0 \Rightarrow \frac {d^2\ell}{d\theta^2}<0\)
所以,求获得 \(\ell(\theta|data)\) 最大值的 \(\theta\) 即可令 \(L(\theta|data)\) 获得最大值。
12.5 极大似然估计的性质
极大似然估计 (maximum likelihood estimator, MLE):
- 渐进无偏 Asymptotically unbiased:
\(n\rightarrow \infty \Rightarrow E(\hat{\Theta}) \rightarrow \theta\) - 渐进最高效能 Asymptotically efficient:
\(n\rightarrow \infty \Rightarrow Var(\hat{\Theta})\) 是所有参数中方差最小的估计 - 渐进正态分布 Asymptotically normal:
\(n\rightarrow \infty \Rightarrow \hat{\Theta} \sim N(\theta, Var(\hat{\Theta}))\) - 变形后依然保持不变Transformation invariant:
\(\hat{\Theta}\) 是\(\theta\) 的MLE时\(\Rightarrow g(\hat{\Theta})\) 是$g() $ 的MLE - 信息足够充分 Sufficient:
\(\hat{\Theta}\) 包含了观察数据中所有的能够用于估计参数的信息 - 始终不变consistent:
\(n\rightarrow\infty\Rightarrow\hat{\Theta}\rightarrow\theta\) 或者可以写成:\(\varepsilon>0, lim_{n\rightarrow\infty}P(| \hat{\Theta}-\theta|>\varepsilon)=0\)
12.6 率的似然估计
率的似然估计 Likelihood for a rate
如果在一项研究中,参与者有各自不同的追踪随访时间(长度) ,那么我们应该把事件(疾病) 的发病率用率的形式(多少事件每单位人年, e.g. per person year of observation) 。如果这个发病率的参数用 \(\lambda\) 来表示,所有参与对象的随访时间之和为 \(p\) 人年。那么这段时间内的期望事件(疾病发病) 次数为:\(\mu=\lambda p\)。假设事件(疾病发病) 发生是相互独立的,可以使用泊松分布来模拟期望事件(疾病发病) 次数 \(D\):
\[D\sim Poi(\mu)\]
假设我们观察到了 \(D=d\) 个事件,我们获得这个观察值的概率应该用以下的模型:
\[Prob(D=d)=e^{-\mu}\frac{\mu^d}{d!}=e^{-\lambda p}\frac{\lambda^dp^d}{d! }\]
因此,\(\lambda\) 的似然方程是:
\[L(\lambda|observed \;data)=e^{-\lambda p}\frac{\lambda^dp^d}{d!}\]
所以,\(\lambda\) 的对数似然方程是:
\[ \begin{aligned} \ell(\lambda|observed\;data) &= \text{log}(e^{-\lambda p}\frac{\lambda^dp^d}{d!}) \\ &= -\lambda p+d\:\text{log}(\lambda)+d\:\text{log}(p)-\text{log}(d!) \\ \end{aligned} \]
解 \(\ell^\prime(\lambda|data)=0\):
\[ \begin{aligned} \ell^\prime(\lambda|data) &= -p+\frac{d}{\lambda}=0\\ \Rightarrow \hat{\lambda} &= \frac{d}{p} \\ \end{aligned} \]
注意: 在对数似然方程中,不包含参数的部分,对与似然方程的形状不产生任何影响,我们在微分对数似然方程的时候,这部分也都自动消失。所以不包含参数的部分,与我们如何获得极大似然估计是无关的。因此,我们常常在写对数似然方程的时候就把其中没有参数的部分直接忽略了。例如上面泊松分布的似然方程中,\(d\:\text{log}(p)-\text{log}(d!)\) 不包含参数 \(\lambda\) 可以直接不写出来。