第 10 章 IRT项目参数估计
由于测试中项目参数的实际值是未知的,需要估计模型中的参数。下面将假定在考生能力已知的情况下估计单个项目的参数。实际上这些分数是未知的,做出此假设是为了能简单的理解项目参数的估计过程。
10.1 项目参数的估计(Estimation of Item Parameters)
在典型测试的中,\(N\) 个考生对测试中的 \(J\) 个项目作出响应,这些考生的能力分数分布在能力量表上。将这些考生按能力分数分为\(G\)组,每组中的\(f_{g}\)个考生有相同的能力水平\(\theta_{g}\)。在一个组中,\(r_{g}\)个考生能正确作答给定项目。因此,在能力水平 \(\theta_{g}\)下,观察到的正确响应比例为\(p\left(\theta_{g}\right)=r_{g} / f_{g}\),即为观测到的该能力水平下正确反应概率。对每个能力组,都可以计算\(p(\theta_{g})\)。如果绘制每个能力组中观察到的正确响应的比例的散点图,结果类似于下图 10.1所示。
双参数ICC模型拟合上图,利用最大似然法(MLE,maximum likelihood estimation)估计参数时,先确定一组初始值,通过ICC曲线方程计算每个能力水平上的\(P(\theta_{g})\),不断调整参数\(b,a\),使ICC曲线与散点图更好的拟合。拟合一致性可以用卡方拟合优度指数(the chi-square bgoodness-of-fit index)来衡量: \[\chi^{2}=\sum_{g=1}^{G} f_{g} \frac{\left[p\left(\theta_{g}\right)-P\left(\theta_{g}\right)\right]^{2}}{P\left(\theta_{g}\right) Q\left(\theta_{g}\right)}\] 其中,\(p(\theta_{g})\)是观察到的第g组正确响应比例,\(P(\theta_{g})\)是使用估计参数从项目特征曲线模型计算的第g组的正确响应概率,\(Q\left(\theta_{g}\right)=1-P\left(\theta_{g}\right)\)。
图 10.2 是与图 10.1 中所示的观察到的正确响应比例相拟合的ICC曲线。
其参数的估计值\(b=-0.32,a=1.31,\chi^{2}=30.02\)。
- 卡方检验临界值(0.05显著性水平)
- Rasch model: \(\chi^{2}(G-1)\)
- 双参模型: \(\chi^{2}(G-2)\)
- 三参模型: \(\chi^{2}(G-3)\)
可用R语言计算:qchisq(.95, df=f)
## [1] 44.9853410.2 使用 Logistic回归估计双参IRT模型参数
R语言glm逻辑回归估计参数(glm的R函数中使用最小二乘法)。
逻辑回归模型: \[P\left(\theta_{g}\right)=\frac{1}{1+\exp \left[-\left(\beta_{0}+\beta_{1} \theta_{g}\right)\right]}\] 双参数IRT模型: \[P(\theta)=\frac{1}{1+e^{-L}}=\frac{1}{1+e^{-a(\theta-b)}}\] 因此,在双参数IRT模型中\(a \equiv \beta_{1}, b \equiv-\beta_{0} / \beta_{1}\)
set.seed(1)
theta <- seq(-3, 3, .1875)
f <- rep(21, length(theta)) # 模拟能力值范围-3到3的33个组,每组21个考生
wb <- -0.39
wa <- 1.27
for (g in 1:length(theta)) {
P <- 1 / (1 + exp(-wa * (theta - wb))) # 难度wb,区分度wa下,不同theta的正确响应概率
}
r <- rbinom(length(theta), f, P) # 随机生成正确响应的考生人数
p <- r / f # 观测的正确响应概率
plot(theta,p, xlab="Ability",ylab="Probability of Correct Response") 
图 10.1: 观察到的正确反应比例与能力的关系散点图
fit <- glm(cbind(r,f-r) ~ theta, family=binomial) # glm估计参数
ahat <- summary(fit)$coefficients[2]
bhat <- -summary(fit)$coefficients[1]/summary(fit )$coefficients[2]
chi_squ <- sum(f*((p-P)^2)/(P*(1-P))) # 卡方检测
plot(theta, p, xlim=c(-3,3), ylim=c(0,1),
xlab="Ability", ylab="Probability of Correct Response",
main= paste0('Chi-square= ',round(chi_squ,2),"\n","a= ",round(ahat,2),", b= ",round(bhat,2)))
lines(theta,P)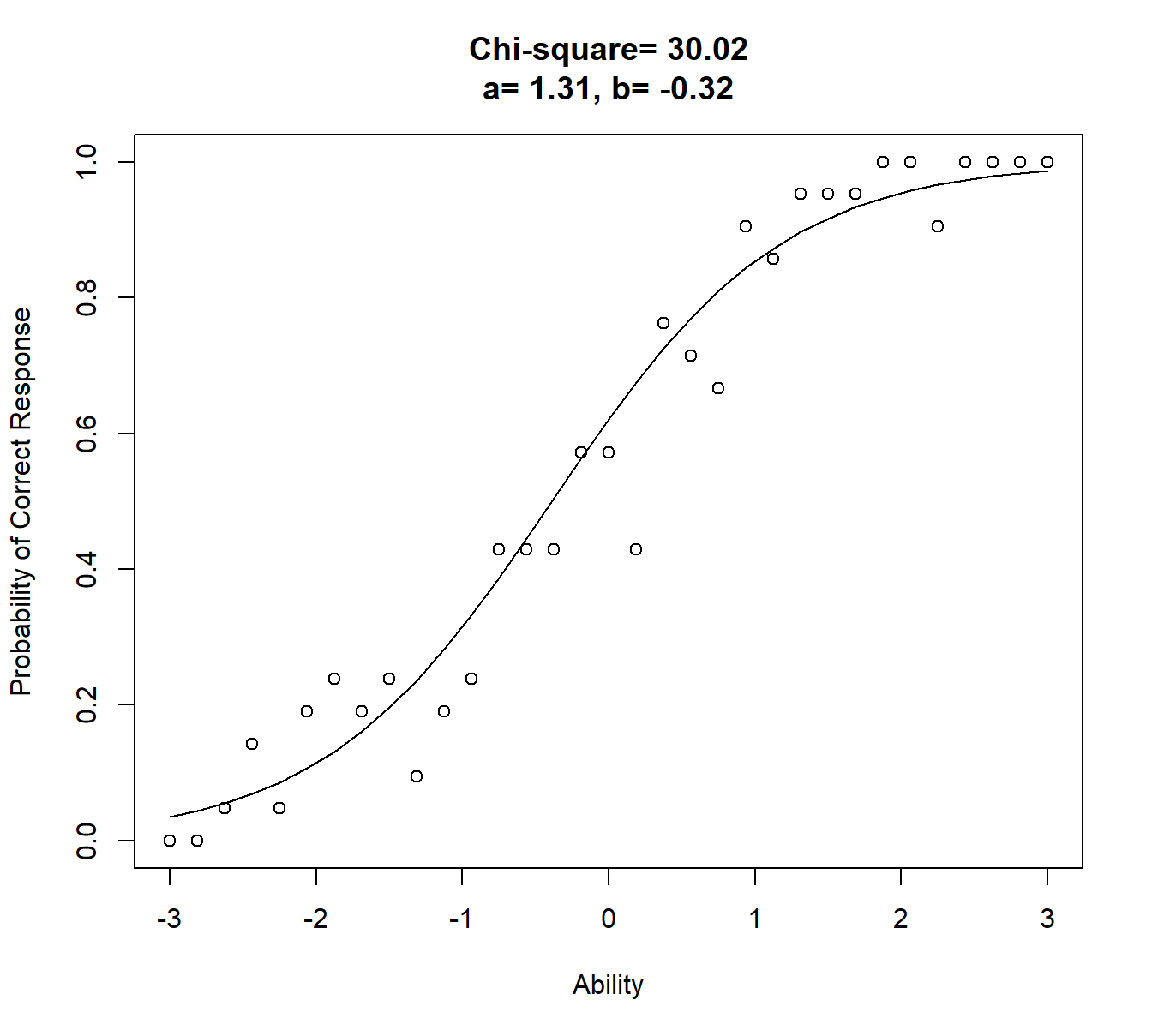
图 10.2: 正确反应比例与能力的关系的ICC拟合
10.3 项参数的组不变性(The Group Invariance of Item Parameters)
项目反应理论的一个有趣特征是项目参数不依赖于考生对项目作出反应的能力水平,即项目参数具有组不变性(Group Invariance)。具体描述如下:假设有两组考生来自相同的考生群体,第一组的能力\(\theta\)范围为-3到-1,均值为-2;第二组能力\(\theta\)范围为+1到+3,均为 +2。根据两组中每个能力水平的项目响应数据计算对给定项目的正确响应的观察比例。然后,对于第一组,正确响应的比例如下。
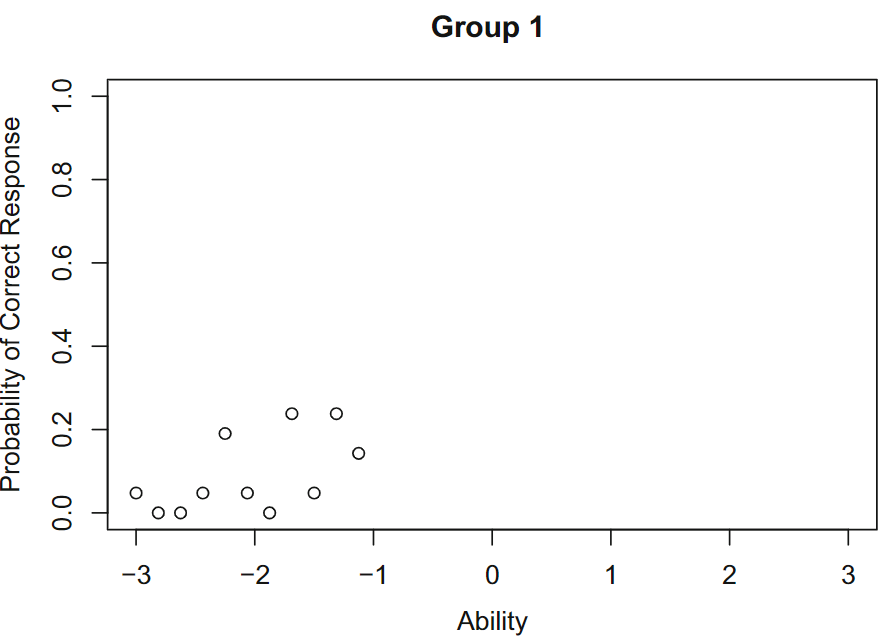 观察到的第 1 组正确响应的比例
观察到的第 1 组正确响应的比例
然后使用最大似然估计进行项目特征曲线拟合,参数估计值\(b(1)=-0.39,a(1)=1.27\),在第一组包含的能力范围内绘项目特征曲线,如下:
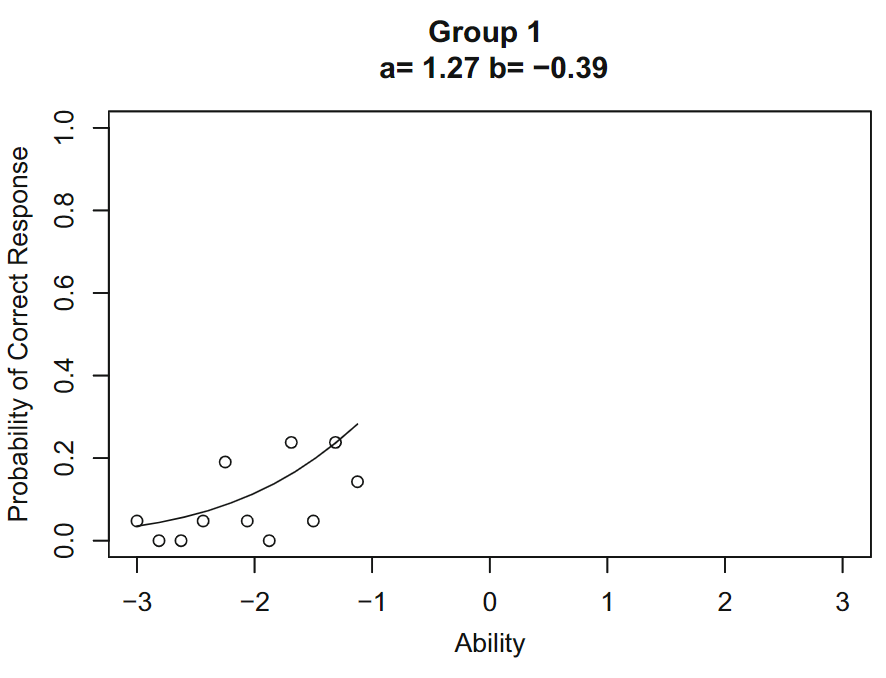 第 1 组项目特征曲线\(b(1)=-0.39,a(1)=1.27\)
第 1 组项目特征曲线\(b(1)=-0.39,a(1)=1.27\)
同样的过程用于第二组
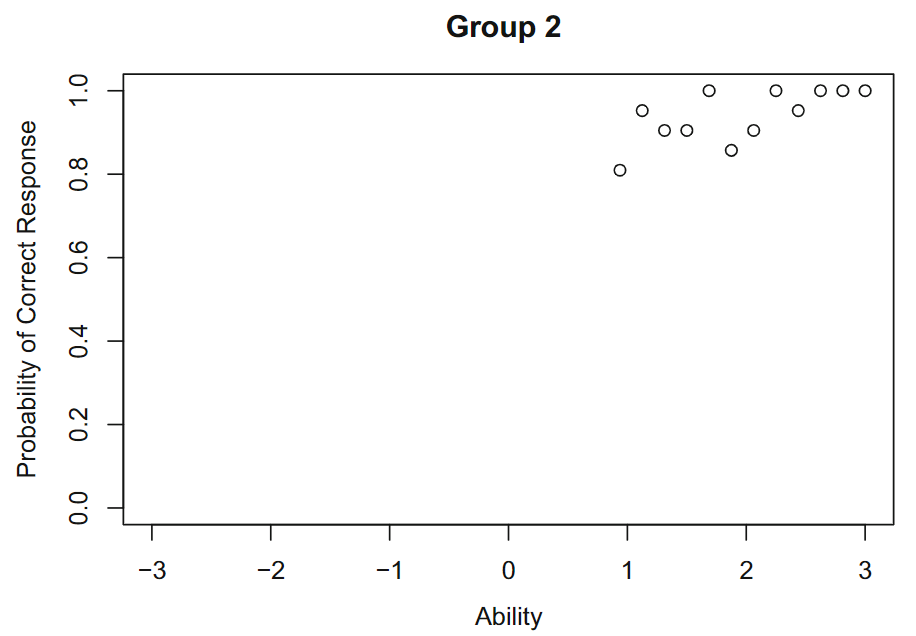 观察到的第 2 组正确响应的比例
观察到的第 2 组正确响应的比例
第二组拟合参数\(b(2)=-0.39,a(2)=1.27\)
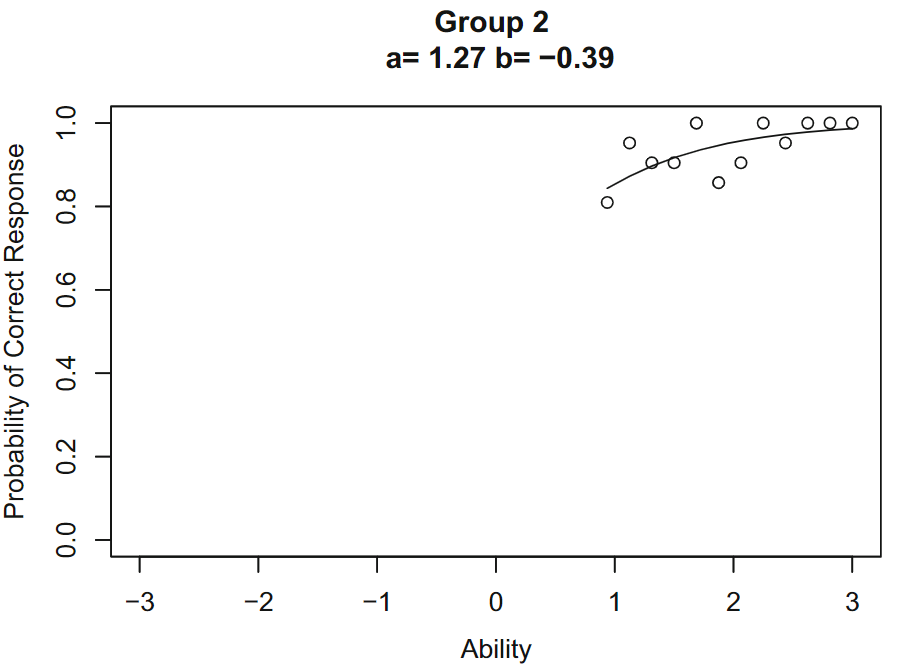 第 2 组项目特征曲线\(b(2)=-0.39,a(2)=1.27\)
第 2 组项目特征曲线\(b(2)=-0.39,a(2)=1.27\)
将两组合并:
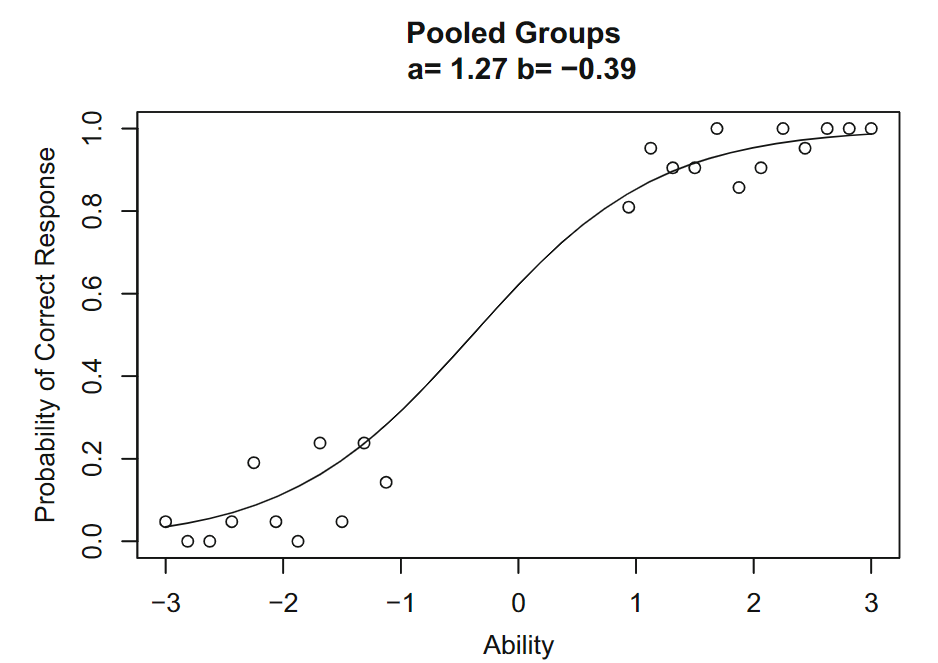 合并两组后项目特征曲线 \(b=-0.39,a=1.27\)
合并两组后项目特征曲线 \(b=-0.39,a=1.27\)
上述即IRT项目参数的组不变性,这是IRT的一个非常强大的特征。它表示项目参数的值是项目本身的属性,而不是响应项目的组的属性。经典测量理论CTT的题目难度是一组考生对一个题目正确回答的总体比例,受考生水平的影响。例如,在IRT中,如果 \(b=0\) 的项目由低能力组回答,则很少有考生会答对;但在CTT中,对于同一题,在低能力组中,难度指数可能为0.3,但在高能力组中可能为0.8。IRT因其组不变性,项目难度更容易解释。
在实际测试情况下,组不变性原则成立。需注意的是,尽管项目参数是组不变的,但并不意味着对于来自同一人群的两组考生通过估计得出的项目参数始终完全相同。因样本大小、数据质量和拟合程度会发生变化,但都它们都应该在同一个范围内。
此外,测试项目必须用于测量两组相同的潜在特征,当测量不同的潜在特征时,或受试者来自测试不适合的人群时,或两组来自两个不同的受试者人群时,测试项目就不具有好的组不变性。