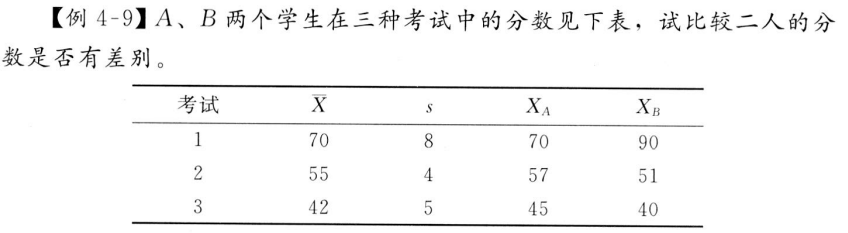
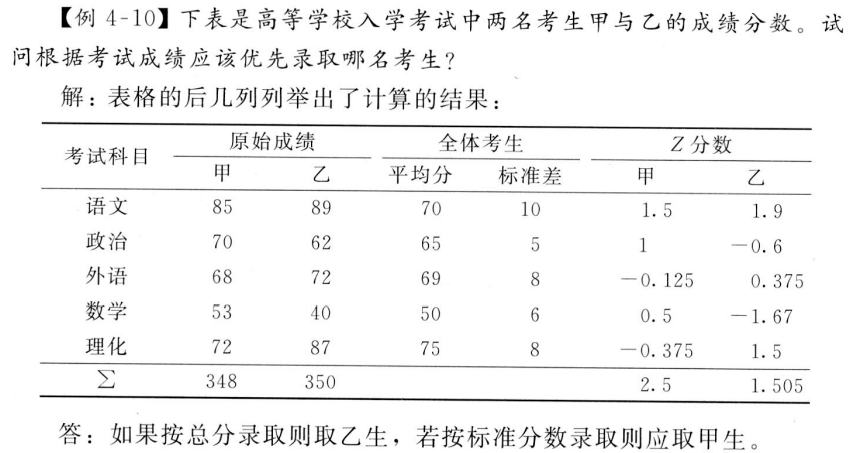
第 2 章 标准差的运用
标准差和方差是典型的差异量数,用途广泛,主要用来描述数据离中趋势,也称为离散量数(measures dispersion)。全距、百分位差和平均差等也属于差异量数,在教育统计过程中一般只用做预备检查,了解数据大致分布范围,不能进一步用于计算。
2.1 百分位差和百分位等级
百分位数(percentile)是指量尺上的一个点,在这个点以下的数据个数占了全部数据个数一定百分比。其符号为\(P_p\)。
- 可利用R语言中
quantile()函数直接计算:
0% 25% 50% 75% 100%
1.0 4.5 8.0 11.5 15.0 25% 75%
4.5 11.5 50%
8 百分等级(percentile rank),是指某个百分位数在整个分数分布中所处的百分位置。
- 计算百分等级:
[1] 0.5[1] 0.252.2 方差和标准差
方差和标准差是表示数据离散程度最好的指标,应用广泛。 根据切比雪夫定理,对于任何数据集,至少有\(1-\frac{1}{h^2}\)的数据落在平均数的\(h\)个标准差内。例如:一组数据平均数为50,标准差为5,则至少有\(1-\frac1{2^2}=\) 75%的数据落在\(50\pm2\times5=35\sim65\)。如果数据呈正态分布,根据中的\(3\sigma\)经验法则,数值分布在\(\sigma\)、\(2\sigma\)、\(3\sigma\)以内的百分比为是68.27%、95.45%和99.73%。
- R语言中
var()计算方差,sd()计算标准差
2.3 标准分数
标准分数也叫\(Z\)分数,计算公式: \[Z = \frac {x-\overline X}{s}\] 式中:\(X\)为某一具体分数,\(\overline X\)为平均数,\(s\)为标准差。
\(Z\)分数是一种具有相等单位的量数。它是将原始分数与团体的平均数之差除以标准差所得的商数,是以标准差为单位度量原始分数离开其平均数的分数之上多少个标准差,或是在平均数之下多少个标准差。它是一个抽象值,不受原始测量单位的影响,并可接受进一步的统计处理。 标准分数在标准化考试统计分析中有重要的作用。为了使各考试分数可比和可加,并能准确地反映每个考生成绩在考试总体中所处位置,必须使它们具有相同的单位和参照点。等值意义相同的分数,在教育统计中称之为标准分数或\(Z\)分数 为了避免\(Z\)分数出现负数或小数点,常对\(Z\)分数进行变换:\[Z' = aZ+b\],\(a,b\)为常数。
2.3.1 计算Z分数
某班依次测验中成绩如下,甲生100分,乙生80分,问这两生\(Z\)分数是多少少。
[1] 56 62 74 94 52 94 97 80 78 44 52 51 81 63 86 70 83 100 63
[20] 87 96 53 79 48 56 63 41 63 92 60 69 76 70 51 90 80 88 46
[39] 83 65 89 79 87 73 72 87 41 69 84 82- 解
set.seed(1)
data <- round(runif(50,40,100))
mean_x <- mean(data)
s <- sd(data)
Z1 <- (100-mean_x)/s # 1.71
Z2 <- (80-mean_x)/s # 0.49
Z1[1] 1.71375[1] 0.4905166 - 解:
- 解: