第 13 章 IRT-信息量
13.1 信息函数 (The Information Function)
统计中信息可定义为估计参数的方差的倒数,估计参数的方差用 \(\sigma^{2}\) 表示,信息量 \(I=\frac{1}{\sigma^{2}}\)。 在IRT中,当对考生能力参数进行估计时,给定能力水平\(\hat{\theta}\)的信息量等于其方差的倒数。如果信息量大,说明可以准确估计出该考生的真实能力。计算不同能力水平下的信息量,可作信息函数图:
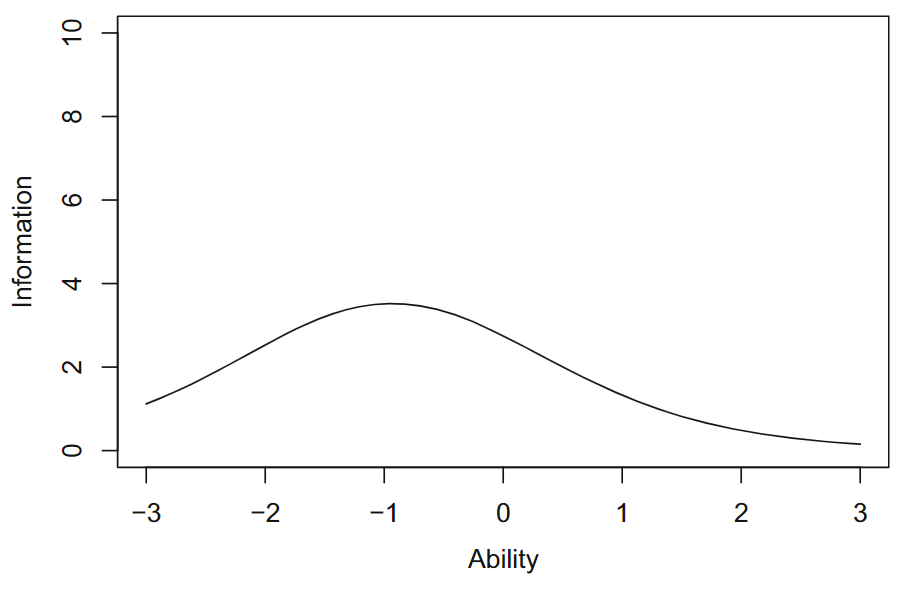 如上图示,在\(-2< \theta<0\)的范围内,信息量大于3,该范围内的能力估计有一定的精度,范围外的信息量迅速减少,能力水平估计精度不高。
如上图示,在\(-2< \theta<0\)的范围内,信息量大于3,该范围内的能力估计有一定的精度,范围外的信息量迅速减少,能力水平估计精度不高。
信息函数叶不依赖于考生在能力量表上的分布。一般在测试中,理想的信息函数是一条水平线,且位于某个较大的 \(I\) 值处,所有能力水平都将以相同的精度进行估计,但很难实现。一般情况下信息函数如上图所示,即不同能力水平的估计精度不同。
13.2 测试信息函数(Test Information Function)
测试中单个项目的信息量有限,包含多个项目的测试的信息量比单个项目信息量高很多,能更准确地衡量考生能力。一次测验中,所有单个项目的信息量总和即为测试信息量 \[I(\theta)=\sum_{j=1}^{J} I_{j}(\theta)\] 其中,\(I(\theta)\) 是能力 \(\theta\) 水平下的测试信息量; \(I_j(\theta)\) 是能力 \(\theta\) 水平下的第 \(j\) 个项目的信息量。
测试信息函数图 13.1 反应测试对能力评估的准确性。单个项目产生的信息量相当小,测试信息量是主要关注点。由于测试信息量是在项目水平上定义的,项目信息量的数学定义取决于所采用的项目特征曲线模型。
信息量与能力估计的可变性之间存在相互关系。将信息量转化为估计的标准误差,只需取测试信息量的平方根的倒数: \[\operatorname{SE}(\theta)=\frac{1}{\sqrt{I(\theta)}}\]
13.3 项目信息的定义
13.3.2 双参数ICC模型
双参ICC模型下,项目信息函数定义为: \[I_{j}(\theta)=a_{j}^{2} P_{j}(\theta) Q_{j}(\theta)\] 其中, \(a_{j}\)为项目第\(j\)个项目的项目区分度参数; \(P_{j}(\theta)=1 /\left[1+\exp \left(-L_{j}\right)\right]\), \(L_{j}=a_{j}\left(\theta-b_{j}\right)\), \(Q_{j}(\theta)=1-P_{j}(\theta)\), \(\theta\)为对应能力等级。
13.3.3 三参数ICC模型
三参ICC模型下,项目信息函数定义为: \[I_{j}(\theta)=a_{j}^{2}\left[\frac{Q_{j}(\theta)}{P_{j}(\theta)}\right]\left[\frac{\left(P_{j}(\theta)-c_{j}\right)^{2}}{\left(1-c_{j}\right)^{2}}\right]\] 其中, \(P_{j}(\theta)=c_{j}+\left(1-c_{j}\right) \times 1 /\left[1+\exp \left(-L_{j}\right)\right]\)
13.3.4 R语言示例
图2测试信息函数示例 假设一项测试包含10个项目,采用双参数ICC模型,项目参数已知。
b <- c(-0.4, -0.3, -0.2, -0.1, 0.0, 0.0, 0.1, 0.2, 0.3, 0.4)
a <- c(1.0, 1.5, 1.2, 1.3, 1.0, 1.6, 1.6, 1.4, 1.1, 1.7)
theta <- seq(-3, 3, 0.1)
J <- length(b)
ii <- matrix(rep(0, length(theta)*J), nrow=length(theta))
i <- rep(0, length(theta))
for (j in 1:J) {
P <- 1 / (1 + exp(-a[j] * (theta - b[j])))
ii[,j] <- a[j]**2 * P * (1.0 - P)
i <- i + ii[,j]
}
plot(theta, i, xlim=c(-3,3), ylim=c(0,10), type="l",
xlab="Ability", ylab="Information"
) 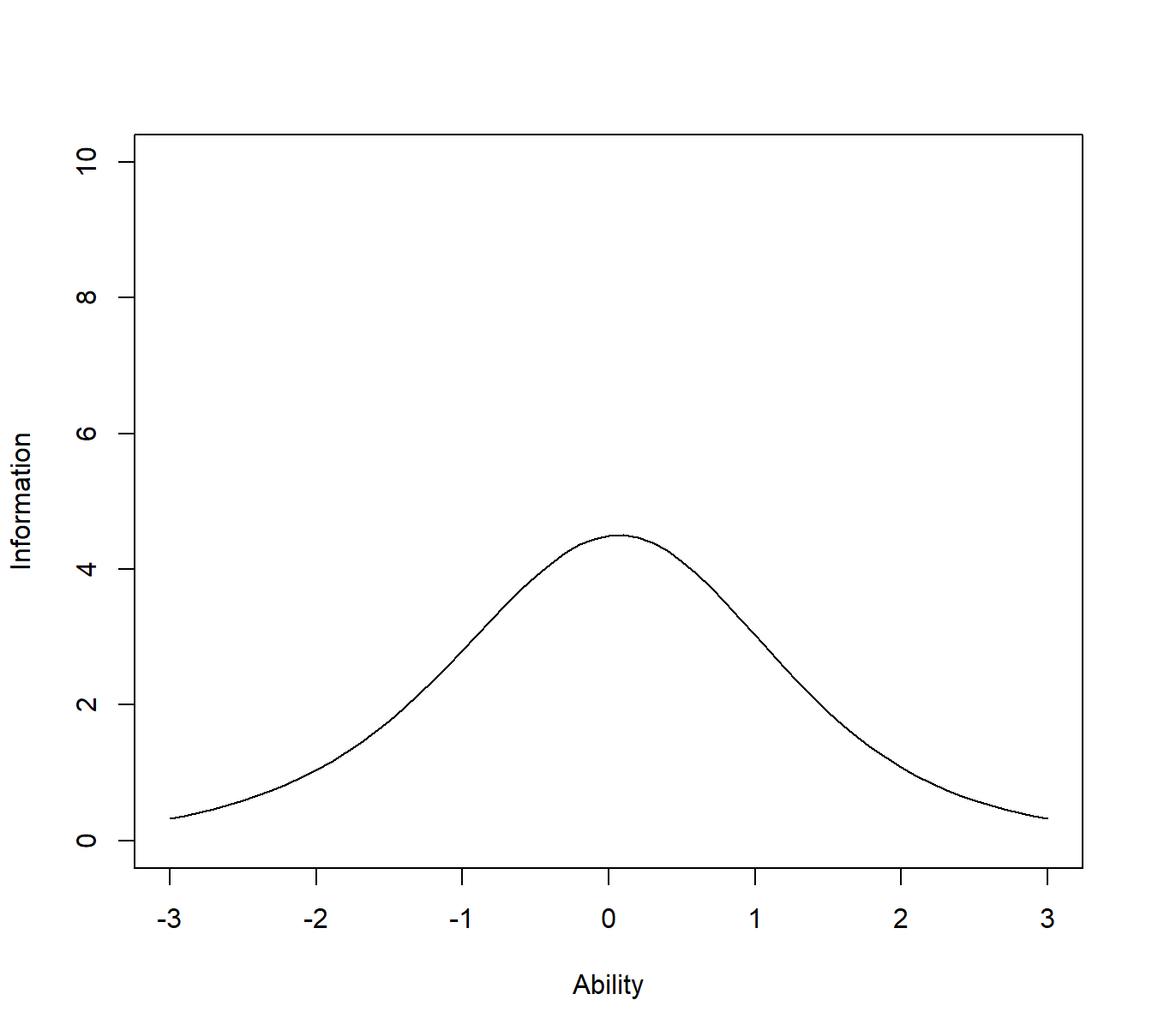
图 13.1: Test Information Function