第 3 章 相关关系的运用
3.1 积差相关
积差相关,又称为皮尔逊相关。使用要求:成对数据,等距或等比性质的两连续变量,正态分布,样本数量大于30。例如每个学生的智力和学习成绩,每个人的身高和体重等。任意两个个体之间不能求皮尔逊相关。
\[r = \frac {\sum xy}{Ns_Xs_Y}\] 式中: \(x,y\)为两变量离均差, \(x = X - \overline X\) \(Y = Y- \overline Y\) \(N\)为成对数据的数目, \(s_X为\)X$变量的标准差, \(s_Y为\)Y$变量的标准差
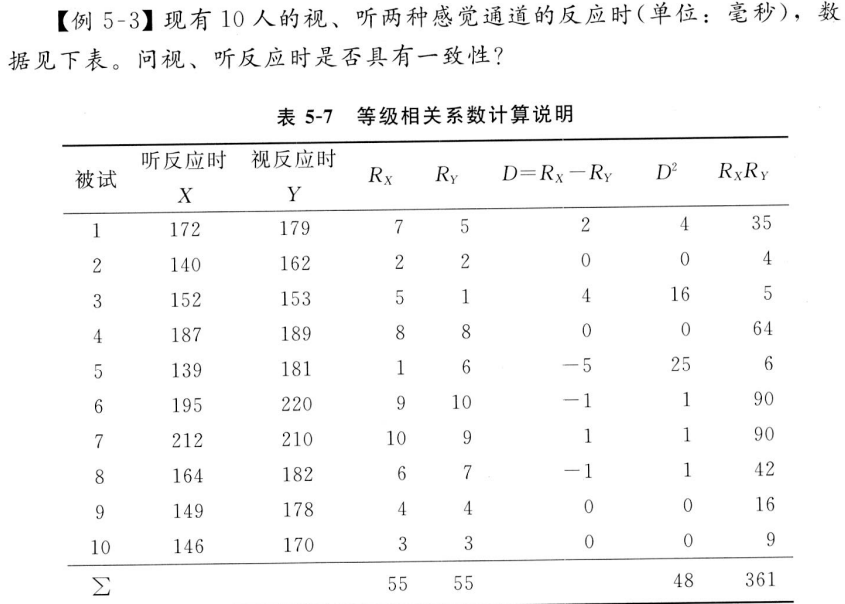
3.2 斯皮尔曼等级相关
斯皮尔曼等级相关。积差相关的延申,精度小于积差相关。使用要求:成对数据,等距或等比性质的两连续变量,数据分布无要求,样本数可小于30。
\[r_R =1- \frac {6{\sum D^2}}{N(N^2-1)}\] 式中: \(N\)为等级个数, \(D\)指二列成对变量的等级差数 。
3.3 肯德尔等级相关
肯德尔等级相关。用字母\(W\)表示,又称为肯德尔和谐系数,功用与斯皮尔曼等级相关相同,适合于两列以上的等级变量。
同一评价者无相同等级评定时,W的计算公式: \[W = \frac {s}{ \frac {1}{12}K^2(N^3-N)}\] 式中: \(s=\sum(R_i-\frac{\sum R_i}{N})^2\); \(R_i代\)表评价对象获得的K个等级之和; \(K\)代表等级评定者数; \(N\)代表被等级评定的对象数目。
同一评价者有相同等级评定时,W的计算公式: \[W = \frac {s}{ \frac {1}{12}K^2(N^3-N)-K \sum T}\] 其中: \(\sum T = \sum\frac{n_{ij}^3-n_{ij}}{12}\),\(n_{ij}\)为第\(i\)个评价者的评定结果中第\(j\)个重复等级的相同等级数。
\(W\)介于0到1之间,W=1表示K个评价者意见完全一致,0<W<1代表K个评价者意见存在一定关系,但不完全一致,W=0表示K个评价者意见完全不一致。
3.3.1 作文评分标准掌握是否一致
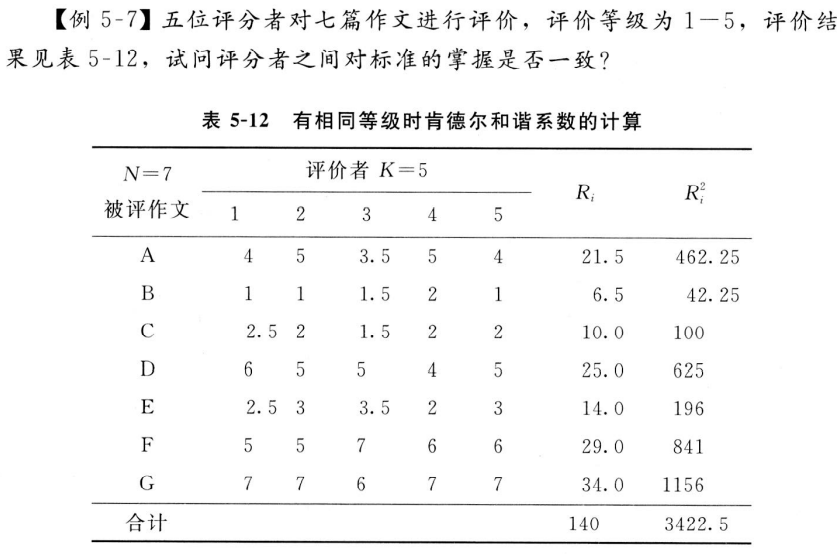
- 解:
data <- data.frame(K1 = c(4,1,2.5,6,2.5,5,7),
K2 = c(5,1,2,5,3,5,7),
K3 = c(3.5,1.5,1.5,5,3.5,7,6),
K4 = c(5,2,2,4,2,6,7),
K5 = c(4,1,2,5,3,6,7)
)
rownames(data) <- LETTERS[1:7]
N <- 7
K <- 5
R_i <- rowSums(sapply(data, rank))
s <- sum( (R_i-sum(R_i)/N)^2 )
# T_ij计算
T_ij <- function(x){
tmp <- table(x)
n <- tmp[tmp >= 2]
T_ij <- (n^3-n)/12
return(as.numeric(T_ij))
}
T_ij_sum <- sum(unlist(sapply(data,T_ij)))
W <- s/(K^2*(N^3-N)/12-K*T_ij_sum)
W[1] 0.9256506\(W = 0.926\) 五位评分这对七篇作文的评价标准比较一致
3.3.2 对颜色喜爱程度是否一致
假设有10人对7种颜色的喜爱程度进行评级,最喜欢为7,最不喜欢为1,结果如下表,问这10人对颜色的爱好是否一致。
- 解:
# 下数据模拟10人对"红","橙","黄"喜爱程度一致,计算W结果为0.84
set.seed(1)
data <- data.frame(K1 = c(7,6,5,sample(1:4,4)),
K2 = c(7,6,5,sample(1:4,4)),
K3 = c(7,6,5,sample(1:4,4)),
K4 = c(7,6,5,sample(1:4,4)),
K5 = c(7,6,5,sample(1:4,4)),
K6 = c(7,6,5,sample(1:4,4)),
K7 = c(7,6,5,sample(1:4,4)),
K8 = c(7,6,5,sample(1:4,4)),
K9 = c(7,6,5,sample(1:4,4)),
K10 = c(7,6,5,sample(1:4,4))
)
# 下数据模拟10人对所有颜色喜爱程度一致,计算W结果为1
# data <- data.frame(K1 = 7:1,
# K2 = 7:1,
# K3 = 7:1,
# K4 = 7:1,
# K5 = 7:1,
# K6 = 7:1,
# K7 = 7:1,
# K8 = 7:1,
# K9 = 7:1,
# K10 = 7:1
# )
#
rownames(data) <- c("红","橙","黄","绿","蓝","青","紫")
data K1 K2 K3 K4 K5 K6 K7 K8 K9 K10
红 7 7 7 7 7 7 7 7 7 7
橙 6 6 6 6 6 6 6 6 6 6
黄 5 5 5 5 5 5 5 5 5 5
绿 1 1 2 1 2 3 1 2 4 3
蓝 3 3 3 4 4 1 2 4 3 2
青 4 4 1 2 1 4 4 3 1 4
紫 2 2 4 3 3 2 3 1 2 1N <- 7
K <- 10
R_i <- rowSums(sapply(data, rank))
s <- sum( (R_i-sum(R_i)/N)^2 )
# T_ij计算计算
T_ij <- function(x){
tmp <- table(x)
n <- tmp[tmp >= 2]
T_ij <- (n^3-n)/12
return(as.numeric(T_ij))
}
T_ij_sum <- sum(unlist(sapply(data,T_ij))) # 结果为0 (同一评价者无相同等级评定)
T_ij_sum[1] 0[1] 0.84071433.4 点二列相关
点二列相关。点二列相关多用于评价由是非类测验题目组成的测验的内部一致性等问题。
计算点二列相关(point-biserial correlation)的公式: \[r_{pb} =\frac {\overline X_p - \overline X_q}{s_t}\cdot \sqrt{pq}\] \(\overline X_p\)是与二分称名变量的一个值对应的连续变量的平均数; \(\overline X_q\)是与二分称名变晕的另一个值对应的连续变量的平均数; \(p\)与\(q\)是二分称名变量两个值各自所占的比率, \(p+q= 1\); \(s_t\) 是连续变量的标准差。
3.4.1 测验总分与题目的相关程度
有一是非式选择测验, 每题选对得2分,共有50题,满分100分。 表中是20名学生在该测验中的总成绩及笫5题的选答情况。 问这道题与测验总分的相关程度如何?
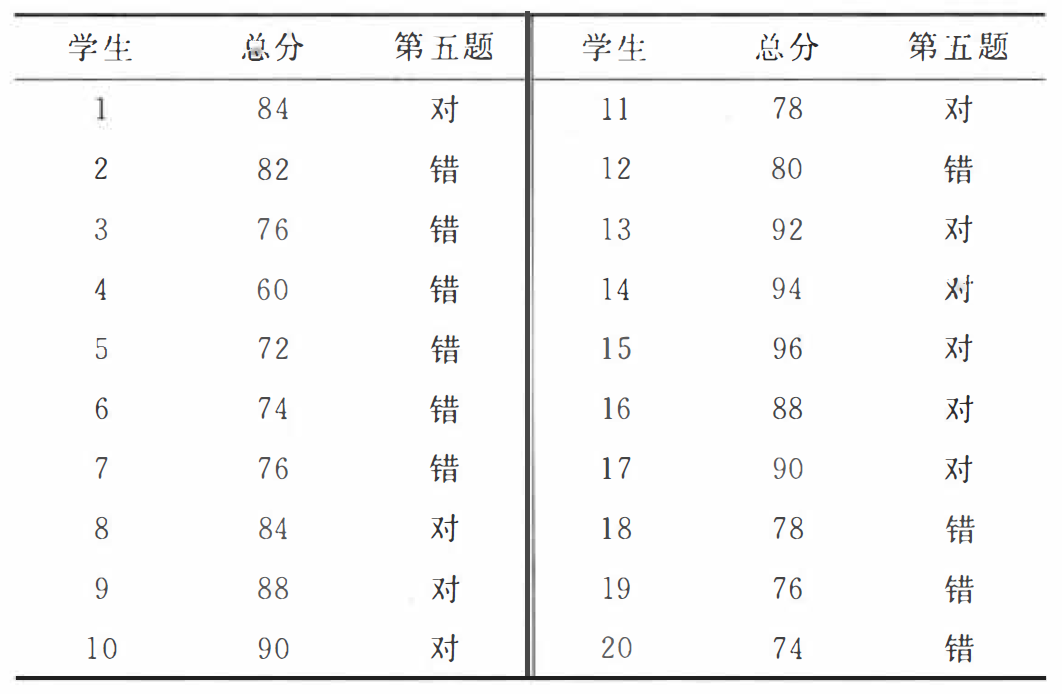
zongfen <- c(84,82,76,60,72,74,76,84,88,90,
78,80,92,94,96,88,90,78,76,74)
timu <- c(1,0,0,0,0,0,0,1,1,1,
1,0,1,1,1,1,1,0,0,0) # 1对 0错
N <- 20
p <- table(timu )["1"]/N # 答对第五题学生比率
q <- table(timu )["0"]/N # 答错第五题学生比率
X_p <- mean(zongfen[timu== 1]) # 答对第五题学生总分平均成绩
X_q <- mean(zongfen[timu == 0]) # 答对第五题学生总分平均成绩
s_t <- sd(zongfen)
r_pb <- (X_p-X_q)/s_t*(p*q)^(1/2)
r_pb 1
0.7651107 第5题与测验总分之间的相关系数为0.76, 相关较高.即第5题的答对答错与总分有一致性,表明第五题的区分度较高。