第 4 章 正态分布的应用
教育统计中,若得到的等级资料属于正态分布,可以将其数量化以便于比较。R语言中pnorm,qnorm函数可用于正态分布的计算。
判断资料否满足正态分布,可以简单的计算峰度和偏度值来判断,R语言中可使用moments包计算偏度skewness和峰度kurtosis;也可采用Shapiro–Wilk(S-W)检验shapiro.test或Kolmogorov-Smirnov(K-S)检验ks.test来判断。
4.1 化等级评定为测量数据
有3位教师对100名学生作等级评定,下表是教师评定结果统计以及其中3位学生获得的评定等级,将其转化为Z分数。
options(digits = 2)
# 模拟等级数据
data <- data.frame(
student = paste0("Student",1:100),
T1 = c(rep("A",5),rep("B",25),rep("C",40),rep("D",25),rep("E",5)),
T2 = c(rep("A",10),rep("B",20),rep("C",40),rep("D",20),rep("E",10)),
T3 = c(rep("A",20),rep("B",25),rep("C",35),rep("D",15),rep("E",5))
)
rating <- data.frame( T1 = c("B","A","D"),
T2 = c("A","B","C"),
T3 = c("A","A","C")
)
student_all <- paste0("Student",1:3)
rownames(rating) <- student_all
teacher_all <- colnames(rating)
head(data) student T1 T2 T3
1 Student1 A A A
2 Student2 A A A
3 Student3 A A A
4 Student4 A A A
5 Student5 A A A
6 Student6 B A A T1 T2 T3
Student1 B A A
Student2 A B A
Student3 D C C从表中可以看到,表面上学生1和学生2的等级相同,都是两个A,1个B,学生3最差。但注意到三位教师中T1只给出5个A等,评定较严,T3给出20个A等,评定较宽。所以学生虽然获得的等级相同,但其价值并不一样,必须将评定等级转化为测量数据。
一般情况下学生等级可以直接转换为标准分数Z比较,步骤如下: 1. 统计每位评价者打出的不同等级的比率; 2. 求各等级比率的中间值作为该等级的中点,计算中点以上(或以下)的累加比率; 3. 用累加比率求对应的标准正态分布Z值; 4. 求被评价者Z值算术平均值。
# 统计各评价者等级比率
data_frq <- sapply(data[,-1], table)
data_prop <- prop.table(data_frq ,2)
# 计算累加比率
cum_p <- apply(data_prop,2,function(x){
p <- c()
for (i in 1:length(x)) {
p <- c(p,x[i]/2+sum(x[-1:-i]))
}
return(p)}
)
# 用累加比率求对应的标准正态分布Z值
ratingsorce <- qnorm(cum_p)
zsorce <- matrix(nrow = nrow(rating ),ncol = ncol(rating),dimnames = list(student_all,teacher_all ))
for ( t in teacher_all) {
for (s in student_all) {
zsorce[s,t] <- ratingsorce[rating[s,t],t]
}
}
# 被评价者Z值算术平均值
result <- apply(zsorce , 1, mean)
result## Student1 Student2 Student3
## 1.29 1.36 -0.42学生1和学生2评定等级相同,但二者Z分数不同。
4.2 确定测验题目难易度
测验题目的难易度一般用答题者通过率来确定,但百分数不等距,不能直接用来比较题目间的难度大小,需要将通过率转换成难度分数,以便于比较题目难易差异。
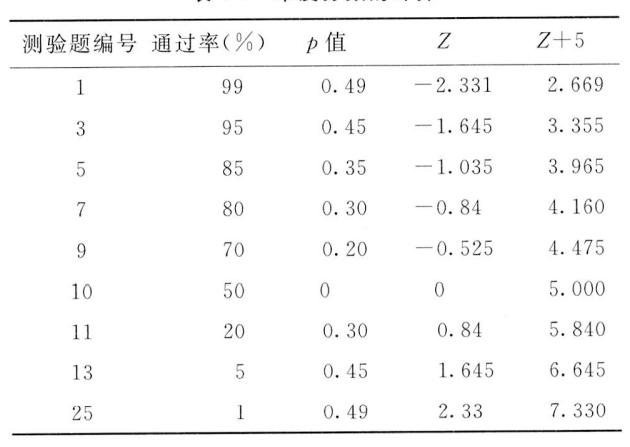
pass <- c(0.99,0.95,0.85,0.80,0.70,0.50,0.20,0.05,0.01)
# 通过率小于50%的Z值计为正值,通过率大于50%的Z值计为正值
zsorce <- qnorm(pass)
zsorce[pass < 0.5] <- abs(zsorce[pass < 0.5])
zsorce[pass > 0.5] <- -abs(zsorce[pass > 0.5])
zsorce <- zsorce + 5
zsorce## [1] 2.7 3.4 4.0 4.2 4.5 5.0 5.8 6.6 7.3