第 9 章 项目特征曲线模型
ICC常用三个数学模型来表示,每个模型采用一个或多个项目参数。
9.1 双参数模型(The Two-Parameter Model)
在IRT理论下,ICC的标准数学模型是 logistic函数的累积形式 Logistic 函数于 1844 年由 Pierre François Verhulst 首次推导出来, 1950 年代后期首次被用作 ICC项目特征曲线的模型,并且由于其简单性,已成为首选模型。双参数逻辑模型: \[P(\theta)=\frac{1}{1+e^{-L}}=\frac{1}{1+e^{-a(\theta-b)}}\] 其中: \(b\)表示项目难度; \(a\)表示项目区分度(Item Discrimination); \(L=a(\theta-b)\)是是逻辑偏差(logit); \(\theta\)表示能力水平。
项目难度参数,用\(b\) 表示,定义为能力量表上对项目做出正确反应的概率为 0.5的点。该参数值的理论范围是 \(-\infty \leq b \leq+\infty\),实践中,通常情况取值范围 为\(-3 \leq b \leq3\)。
ICC曲线的斜率随着能力水平\(\theta\)的变化而变化,并在\(\theta=b\)时达到最大值,定义该处的斜率来表示项目区分度。在双参数模型下,\(\theta=b\)处的实际斜率是\(a/4\),将\(a\) 视为\(b\)处的斜率是可接受的近似值,因此参数\(a\)用于表示项目区分度参数。该参数值的理论范围是\(-\infty \leq a \leq+\infty\) ,实践中常取 \(-2.8 \leq b \leq2.8\)。
9.2 The Rasch Model
Rasch模型由丹麦数学家 Georg Rasch提出。该模型假设所有项目区分度为1,即在双参数模型中,项目参数\(a=1\),只有项目难度参数\(\theta\)可以取不同的值。因此,Rasch 模型通常被称为单参数逻辑模型。 Rasch 模型的方程由下式给出: \[P(\theta)=\frac{1}{1+e^{-1(\theta-b)}}\]
9.3 三参数模型(The Three-Parameter Model)
上述两个模型没有考虑考生在答题过程中猜对题目的情况,Birnbaum (1968) 在双参数逻辑模型基础上增加了一个参数\(c\),该参数表示猜测对题目的概率。在这样的过程中,虽失去了一些逻辑函数的一些数学特性,但由此产生的模型还是称为三参数逻辑模型,三参数模型的方程为: \[P(\theta)=c+(1-c) \frac{1}{1+e^{-a(\theta-b)}}\] 其中,\(c\)表示猜对概率。
要注意的是根据定义,\(c\) 的值不会随着能力水平的变化而变化。因此,能力最低和能力最高的考生通过猜测猜对题目的概率可能相同。参数\(c\) 的理论范围为\(0 \leq c \leq 1.0\),但实际上高于 0.35 的值被认为是不可接受的,在实际中\(0 < c < 0.35\)。
使用猜测参数 \(c\) 使项目难度参数的定义发生了变化。在前两个模型中,项目难度 \(b\) 是能力量表上对项目做出正确反应的概率为 0.5的点。在三参数模型中,ICC曲线下限不为0,而与参数\(c\)有关,\(P(\theta)\)范围 \(c \leq P(\theta) \leq 1.0\),项目难度 \(b\) 对应能力量表上项目做出正确反应的概率为\(P(\theta)=c+(1-c)(0.5)=(1+c) / 2\)的点。
三参数模型中,仍用\(a\)表示项目区分度,但\(\theta=b\)处的实际斜率是\(a(1-c)/4\)。
项目参数 b 和 a 定义的这些变化看起来很小,但在解释测试分析结果时很重要。
9.4 负区分度(Negative Discrimination)
大多数测试项目都会以积极的方式(positive manner)进行区分,即随着能力水平的提高,正确反应的概率增加,但一些项目具有负区分度。在此类项目中,正确回答的概率随着能力水平从低到高的增加而降低。如图 9.1
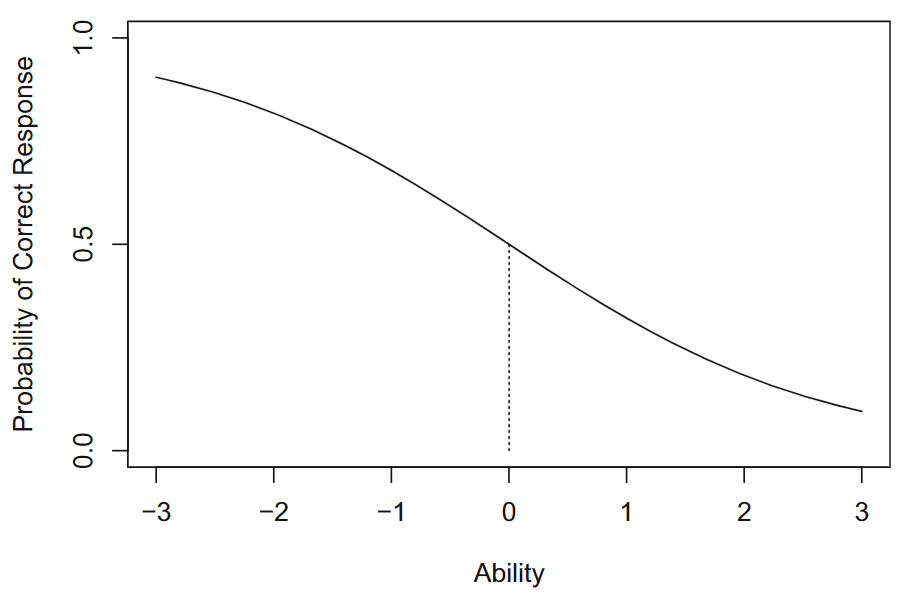
图 9.1: 双参数ICC(b= 0, a= -0.75)
通常情况下区分度应为正值,出现负值说明测试项目可能存在问题。
9.5 项目参数的口头术语(Verbal Terms)
9.5.2 项目难度参数
根据经典测试理论,项目难度是相对于一组考生定义的。同一项目可能对一组人来说很容易,而对另一组人却很难。根据IRT理论,项目的难度是能力量表上正确回答概率为0.5的点(三参数模型为\((1+c) / 2\)的点)。 解释项目难度参数的方法是根据项目在能力量尺上的作用。项目特征曲线的斜率在项目难度参数对应的能力等级处最大,即项目可最大化的区分处于该能力水平附近的考生,因为可以说该项目在这一能力水平上发挥作用。例如,难度为-1的项目在能力较低的考生中发挥作用, +1 表示在较高能力的考生中起作用。 三参数模型下,猜测参数c的数值直接解释为概率。例如,c=0.12 仅表示在所有能力水平下,正确猜测题目的概率为0.12。
9.6 R语言ICC
icccal <- function(b, a, c) {
if (missing(c)) c <- 0
if (missing(a)) a <- 1
theta <- seq(-3, 3, 1)
L <- a * (theta - b)
expnl <- exp(-L)
opexpnl <- 1 + expnl
P <- c + (1 - c) / opexpnl
data.frame(theta, L, expnl, opexpnl, P)
}
icc <- function(b, a, c) {
if (missing(c)) c <- 0
if (missing(a)) a <- 1
par(lab=c(7,3,3))
theta <- seq(-3, 3, .1)
P <- c + (1 - c) / (1 + exp(-a * (theta - b)))
plot(theta, P, type="l", xlim=c(-3,3), ylim=c(0,1),
xlab="Ability", ylab="Probability of Correct Response")
thetai <- b
pthetai <- c + (1 - c) / (1 + exp(-a * (thetai - b)))
vliney <- seq(0, pthetai, .01)
vlinex <- b + vliney * 0
lines(vlinex, vliney, lty=2)
}
icccal(b=-1.0, a=1.7)## theta L expnl opexpnl P
## 1 -3 -3.4 29.964100047 30.964100 0.03229546
## 2 -2 -1.7 5.473947392 6.473947 0.15446527
## 3 -1 0.0 1.000000000 2.000000 0.50000000
## 4 0 1.7 0.182683524 1.182684 0.84553473
## 5 1 3.4 0.033373270 1.033373 0.96770454
## 6 2 5.1 0.006096747 1.006097 0.99394020
## 7 3 6.8 0.001113775 1.001114 0.99888746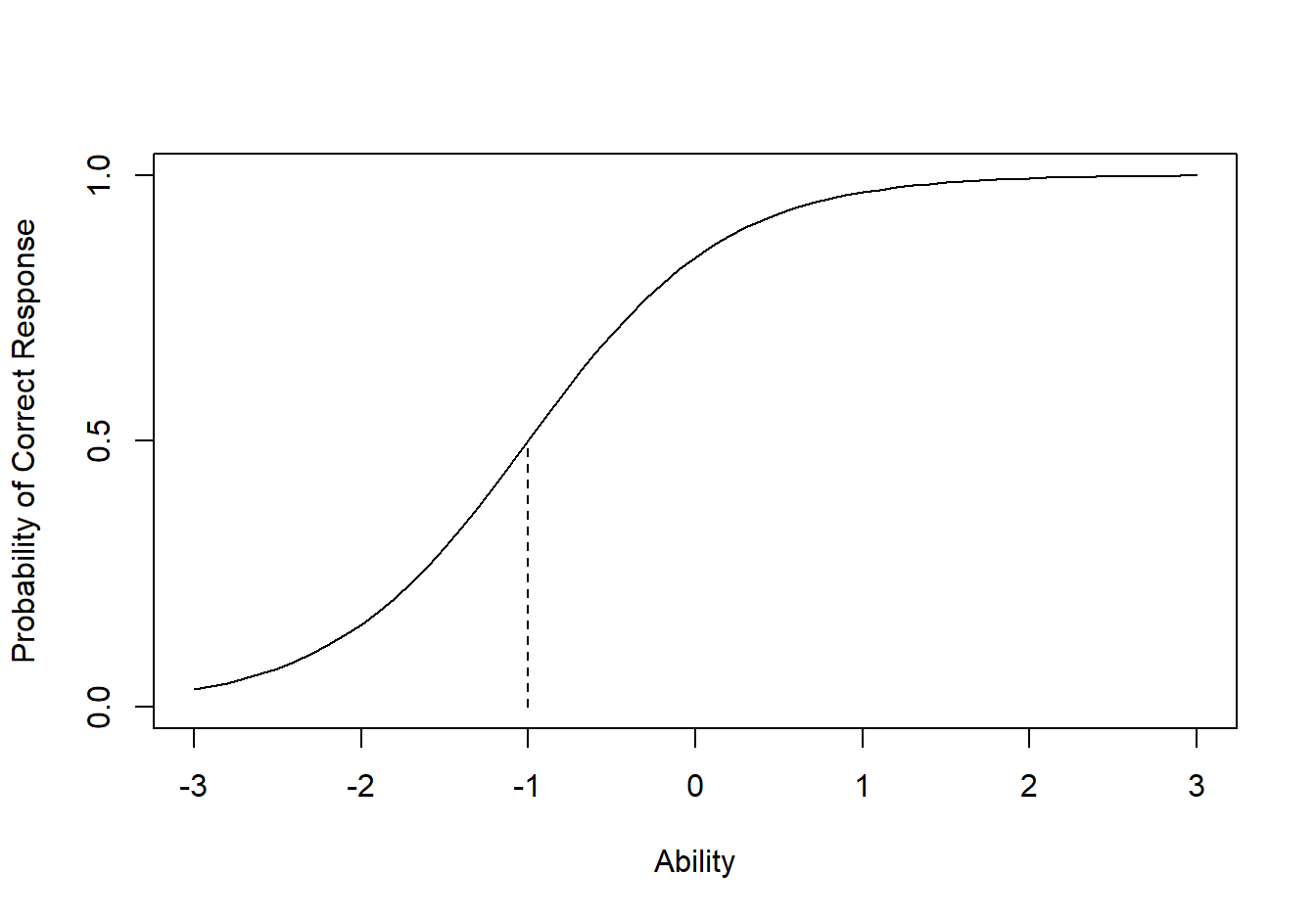
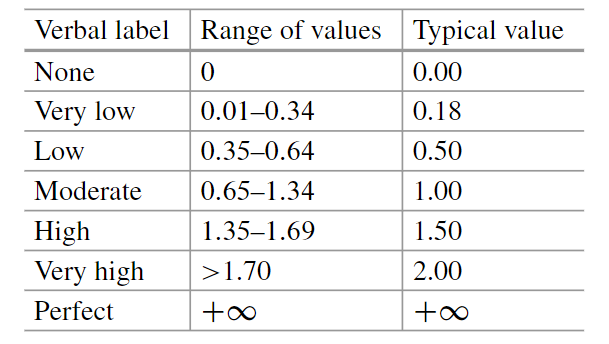 在ICC曲线的逻辑模型下解释项目区分参数时,这些关系成立。若解释正态卵形(normal ogive)模型下的项目区分度参数,对应值除以 1.7。
在ICC曲线的逻辑模型下解释项目区分参数时,这些关系成立。若解释正态卵形(normal ogive)模型下的项目区分度参数,对应值除以 1.7。