第 8 章 项目反应理论 (IRT)
项目反应理论(Item Response Theory, IRT)是一系列心理统计学模型的总称,是针对经典测量理论(Classical Test Theory,简称CTT) 的局限性提出来的。 在许多教育和心理测量情况下都有一个潜在的变量,这个变量往往是可以直观理解的东西,比如“智力”、“阅读能力“和“算术能力”等描述性术语。这些都是不可观察的,潜在的特征。虽然它们很容易描述,但它们不能像身高或体重那样直接测量,因为变量是一个概念而不是物理维度。教育和心理测量的主要目标是确定一个人拥有多少这种潜在特征。由于大多数研究都涉及学术、阅读、数学和算术能力等变量,因此在项目反应理论中使用通用术语“能力”来指代这些潜在特征。 如果要测量一个人具有多少潜在特征,则需要有一个测量尺度。基本思想是,如果可以从物理上确定一个人的能力,则可以使用此标尺来判断一个人具有多少能力,并且可以比较几个人的能力。理论上的能力范围是从负无穷到正无穷,但实际考虑通常将值的范围限制在 3 到 -3 之间。 IRT用学生能力值\(\theta\)与题目难度\(\delta\)的函数来表示学生答对题目的概率。 该函数定义的是一个机率模型,取值介于0到1之间,当学生的能力值越高,所对应的函数值也越高,换句话说,如果学生能力值越高,他答对该题的机率会越高。函数图形近似于S型曲线。
8.1 项目特征曲线(ICC, Item Characteristic Curve)
一个合理的假设是,每个对测试项目做出反应的考生都具有一定程度的潜在能力。因此,可以认为每个考生都有一个能力值分数,用以将考生置于能力量表的某个位置。该能力分数由希腊字母\(\theta\)表示。在每个能力水平上,具有该能力的考生都会有一定的概率给出正确答案。这个概率将用 P. / 表示。对于一个典型的测试项目,这个概率对于能力低的考生来说会很小,而对于能力高的考生来说这个概率会很大。如果将 P./ 绘制为能力的函数,则结果将是一条平滑的 S 形曲线,如图 1.1 所示。正确反应的概率在最低能力水平下接近于零,并增加直到在最高水平能力下正确反应的概率接近统一。这条 S 形曲线描述了对一个项目的正确反应的概率与能力量表之间的关系。在项目反应理论中,它被称为项目特征曲线。测试中的每个项目都有自己的项目特征曲线
根据IRT理论,每个考生都具有一定程度的潜在能力,该能力用字母\(\theta\) 表示 。在每个能力水平上,具有该能力的考生都会有一定的概率给出正确答案。这个概率将用 \(P(\theta)\) 表示。对于一个的测试题目,\(P(\theta)\) 对于能力低的考生来说会很小,对于能力高的考生概率会很大。如果将\(P(\theta)\) 绘制为能力\(\theta\)的函数,则结果将是一条平滑的 S 形曲线,如图 8.1 所示,这条 S 形曲线描述了对一个项目的正确回答的概率与能力之间的关系。在项目反应理论中,它被称为项目特征曲线ICC。测试中的每个项目都有自己的项目特征曲线。
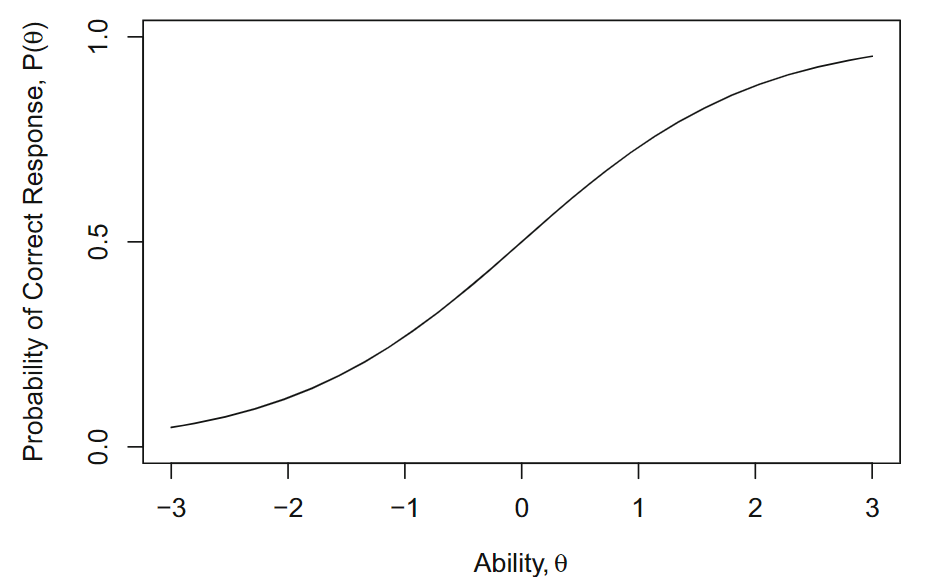
图 8.1: 项目特征曲线(ICC, Item Characteristic Curve)
8.2 项目难度和项目区分度(Item Difficulty and Item Discriminatio)
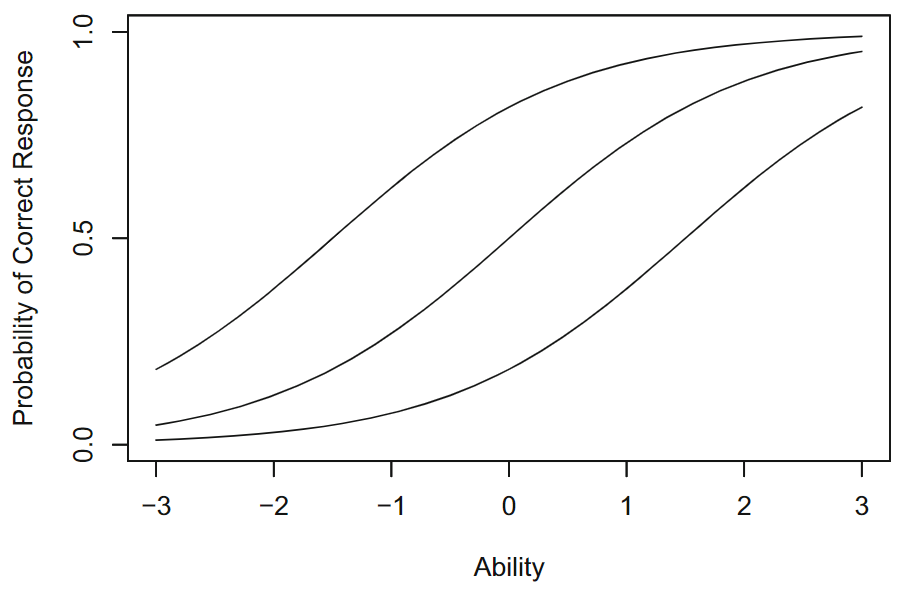
图 8.2: 具有相同区分度但难度不同的三个项目特征曲线
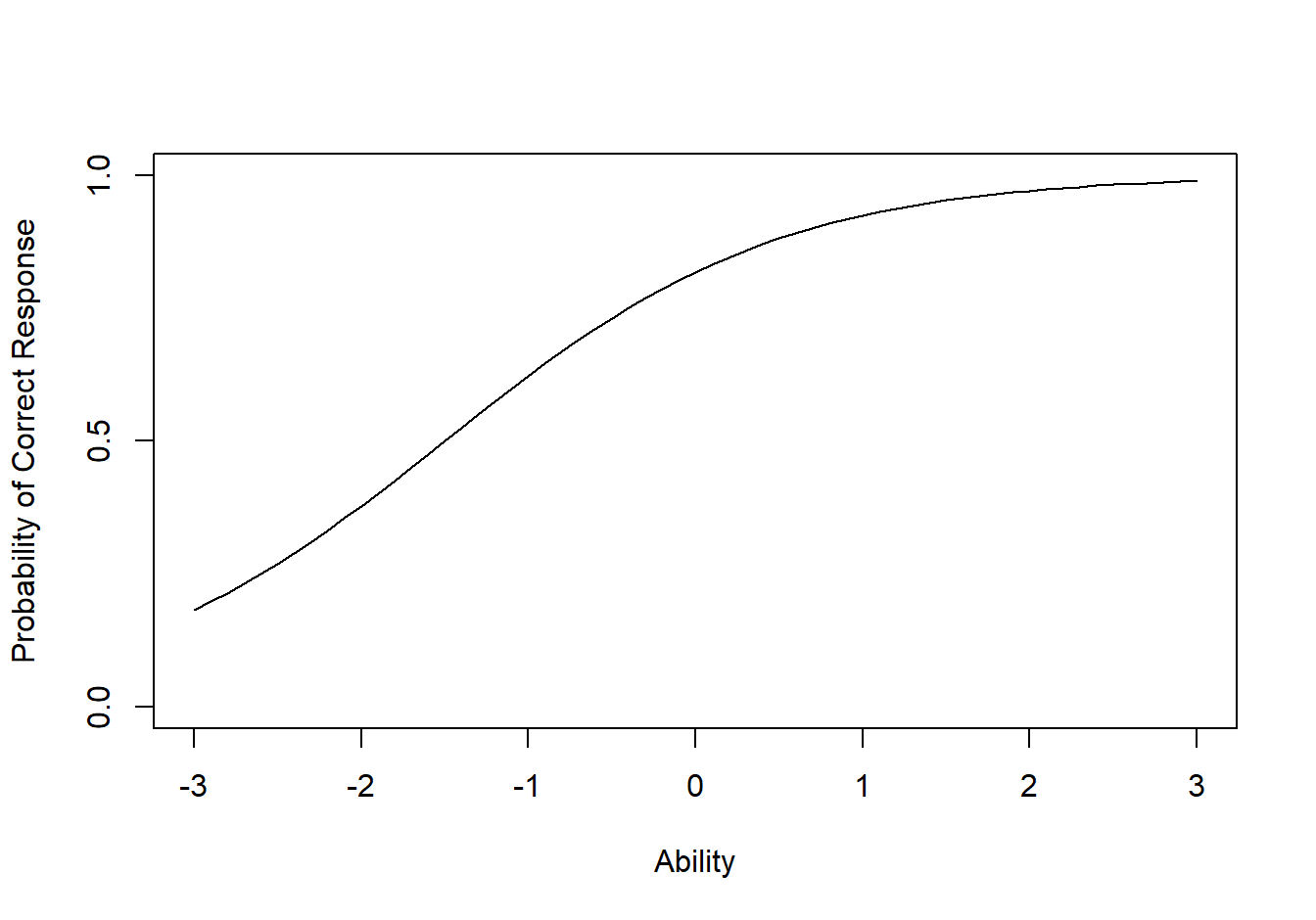
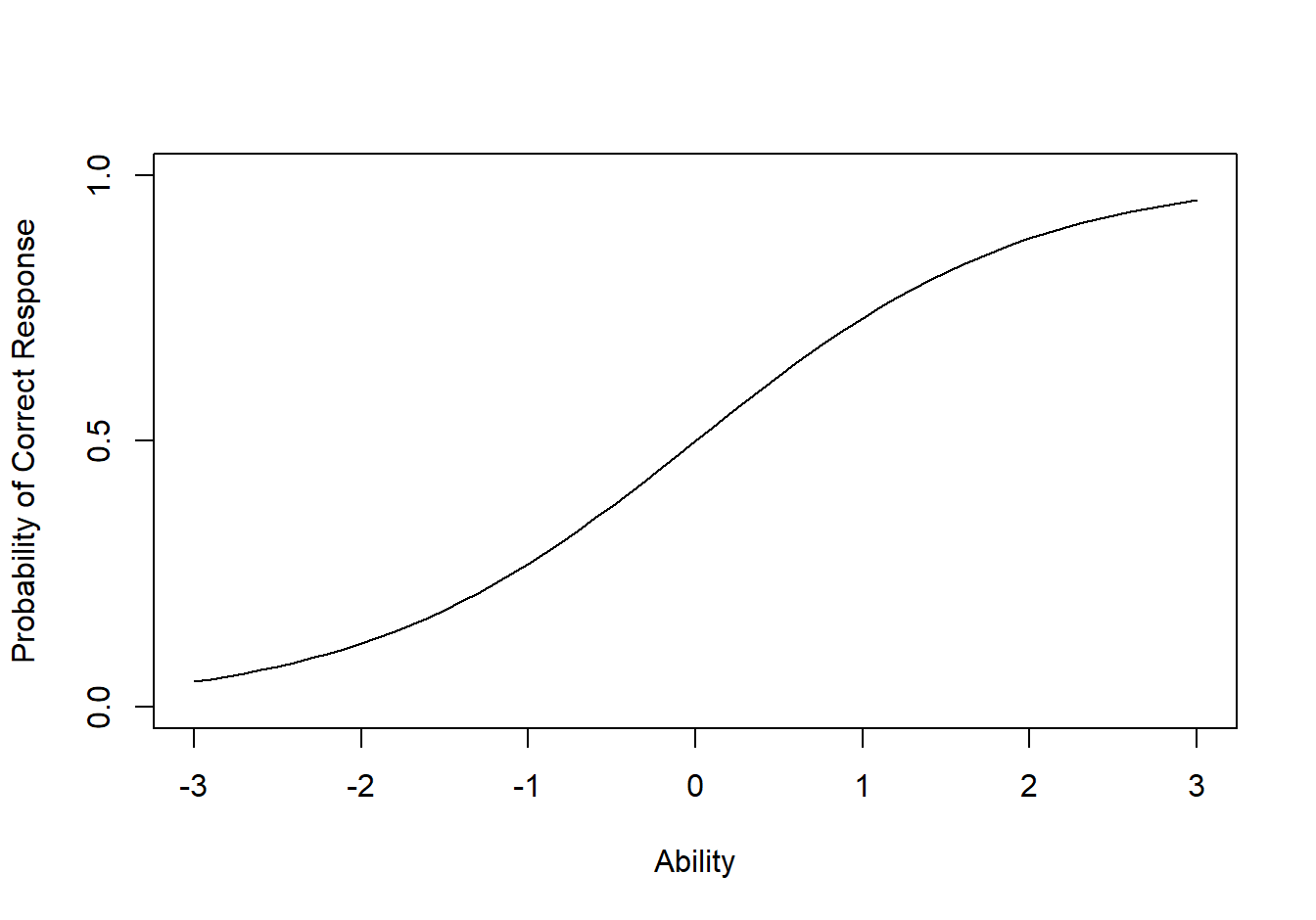
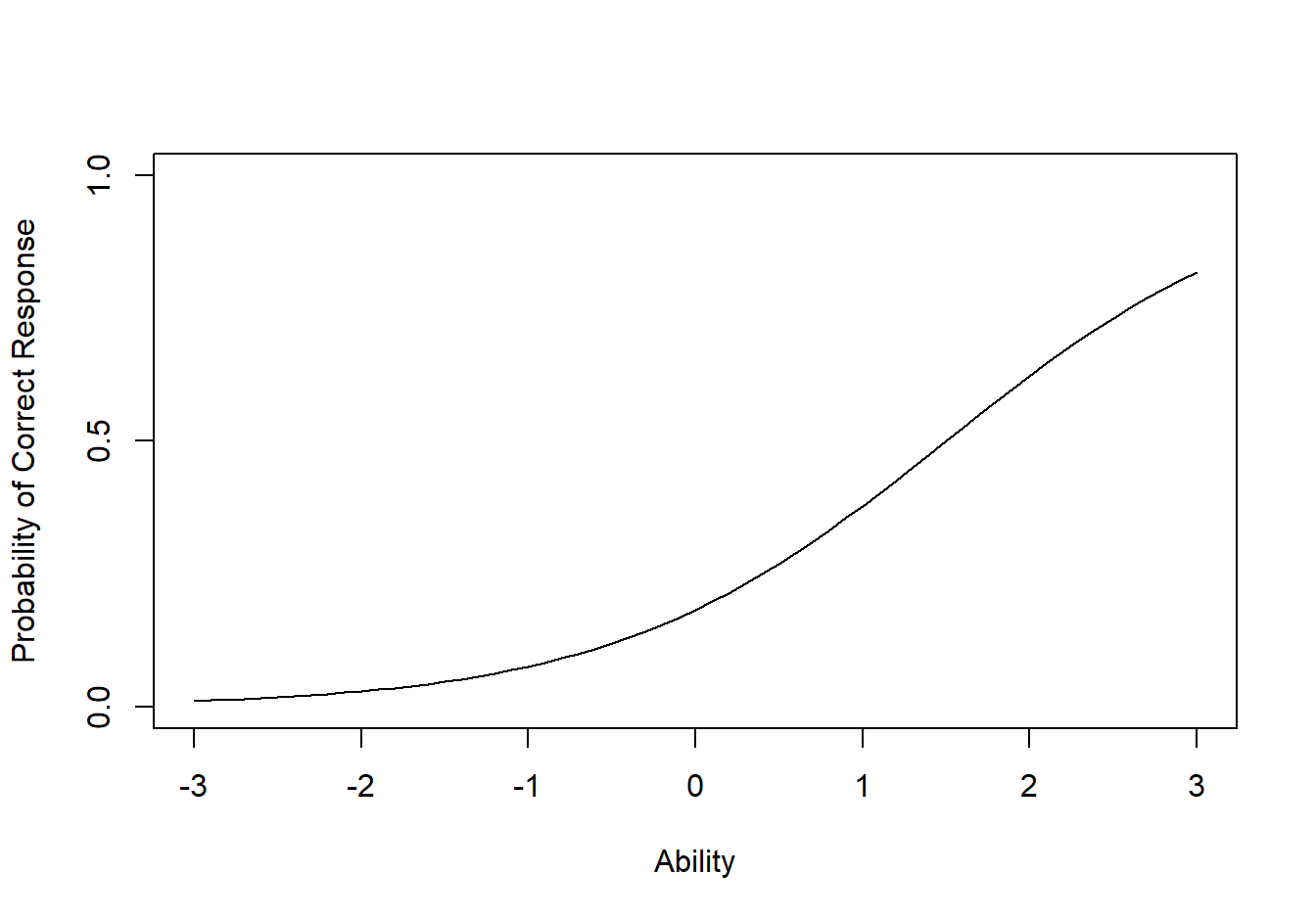
图 8.2,最上边的曲线表示一个简单的项目,因为较低能力考生的正确回答概率很高,而高能力考生的正确回答概率接近 1。中间曲线代表一个中等难度的项目;最下边曲线代表较难项目。对于能力范围大多数在-3到3的考生,回答正确的概率很低,即使在显示的最高能力水平(即\(\theta=3\))下,正确概率仅为 0.8,只有在达到更高的能力水平时才会增加正确概率。
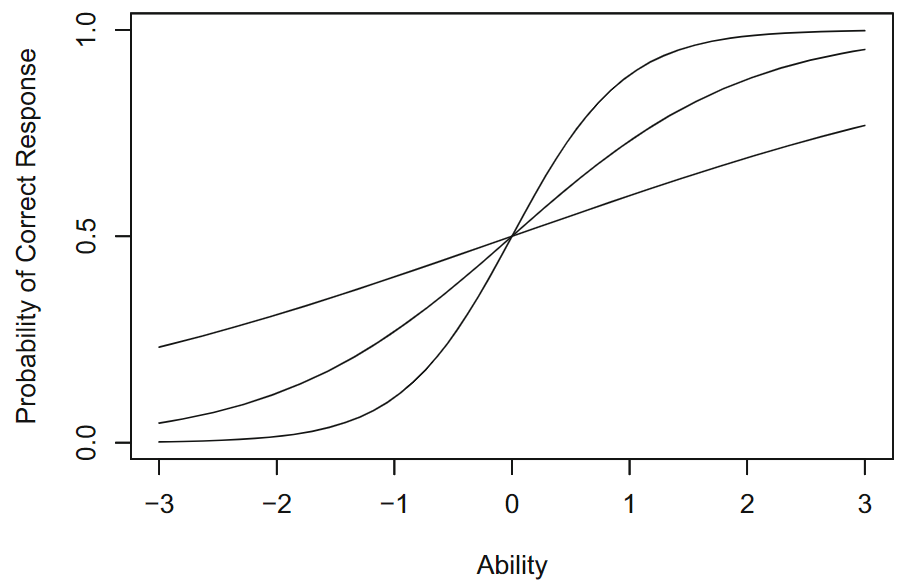
图 8.3: 难度相同但区分度不同的三个项目特征曲线
图 8.3中,正能力范围上方曲线具有高的区分度,该曲线在中间非常陡峭,其中正确响应的概率随着能力的增加而变化非常快。中间曲线代表具有中等项目辨别水平的项目。这条曲线的斜率远小于前一条曲线,并且随着能力水平的提高,正确响应的概率变化也不如前一条曲线那么显着。第三条曲线表示区分度较低的项目。曲线的斜率非常小,正确反应的概率在所示的能力范围内变化缓慢。即使在能力水平较低的情况下,正确反应的概率也相当大,并且只有在达到高能力水平时才会略微增加。
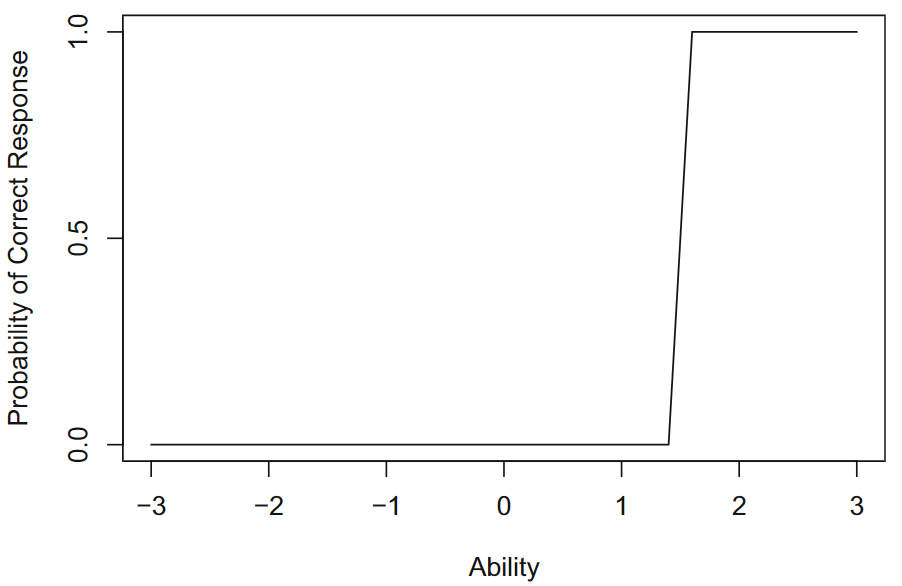
图 8.4: 具有完美辨别力的项目特征曲线
图 8.4 是具有完美辨别力的项目特征曲线。在\(\theta=1.5\)处垂直线的左侧,正确响应的概率为零,而在该线的右侧,正确响应的概率为 1。
因此,该项目完美区分了高于和低于1.5能力得分的考生。但是,该项目对于能力在 1.5 以上的和 1.5 以下的考生没有区别。
8.3 项目难度和项目区分度的口头术语(Verbal Terms)
在项目反应理论的中,为了让对项目特征曲线及其属性有一个直观的理解。项目难度和项目区分度将在口头上定义。 项目难度将有以下等级:
very easy
easy
medium
hard
very hard
项目区分度分以下等级:
none
low
moderate
high
perfect
8.4 R语言绘制不同的项目特征曲线
bveryeasy <- -2.625
beasy <- -1.5
bmedium <- 0
bhard <- 1.5
bveryhard <- 2.625
anone <- 0
alow <- 0.4
amoderate <- 1
ahigh <- 2.1
aperfect <- 999
iccplot <- function(b, a) {
par(lab=c(7,3,3))
theta <- seq(-3, 3, .1)
P <- 1 / (1 + exp(-a * (theta - b)))
plot(theta, P, type="l", xlim=c(-3,3), ylim=c(0,1),
xlab="Ability", ylab="Probability of Correct Response")
}
iccplot(beasy, amoderate)