第 1 章 平均数的运用
几何平均数数,调和平均数都属于平均数,此外还有算术平均数、加权平均数、中数、众数等,它们都可以用来反映数据的集中趋势,统称为集中量数(central tendency)。在教育统计过程中,不同集中量数各有缺点: 算术平均数灵敏,易受极值影响。例如个别低分会影响对整体平均水平的判断。在一些教育心理学实验、学习迁移实验和迷津学习实验观测中,都常会出现极端数情况。 中数计算用不到所有数据,不能进一步计算,受抽样影响较大,不常用。但在心理和教育科研中的实验常不能持续进行、缺少数据或不清楚数据分布情况,中数在这类情况下常被使用。 众数跟中数大体相同。 加权平均数面临权重制定问题。如试题中根据题目难易程度不同赋分,选拔测试中不同科目比例都是加权的体现。但面对复杂教育或心理问题,权重很难确定。
1.1 几何平均数
几何平均数(geometric mean),记作\(Mg\),计算基本公式如下: \[M_g = \sqrt[N] {X_1 \times X_2 \times X_3 \cdots X_N }\] 式中: \(N\)为数据个数;\(X_i\)为变量值。 计算时常用取对数法: \[lgM_g =\frac {\sum lgX_i}N\] 当数据间差异较大,且几乎按一定比例关系变化,例如教育经费的逐年增加,学习、阅读的进步数,学生人数的增长数等。一般不用平均数,而是采用平均增长率,如教育经费的平均年增长率,学校人数的年增长率,学习的平均进步率,阅读速度的平均增加率等,都要用到几何平均数计算平均比率。
1.1.1 学习方面进步率

- 解:
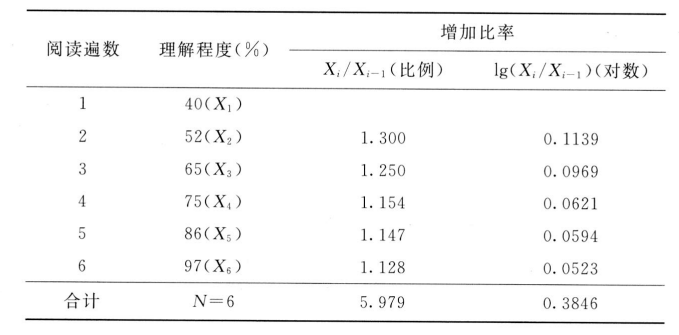
由公式: \(lgM_g = \frac {0.3846}5\)\(=0.07692\) 求反对数: \(M_g=10^{0.07692}=1.19377\) 该实验阅读能力平均进步率为1.19377,平均增加比率为\(1.19377-1=0.19377\)
若以\(X_I=40\)为基数,那么学习第六遍应理解多少? 则\(X_6=40 \times {1.19377^5} =96.97 \approx 97\),若用算数平均数,增加率\(\overline X =\frac {5.979}5=1.1958\),同样以\(X_I=40\)为基数,则\(X_6=40 \times {1.1958^5} =97.8\),比实际理解成份多. 此类问题可简化计算: \[M_g = \sqrt[N-1] {\frac {X_2}{X_1} \times \frac {X_3}{X_2} \times \frac {X_4}{X_3} \cdots \frac {X_N}{X_{N-1}}} = \sqrt[N-1] {\frac {X_N}{X_1}}\]
[1] 1.193831.2 调和平均数
调和平均数(harmonic mead),用符号\(M_H\)表示,在计算中先将各个数据取倒数平均,然后再取倒数,故又称为倒数平均数。计算公式是: \[M_H = \frac {N}{\sum \frac 1X_i}\] 式中: \(N\)为数据个数;\(X_i\)为变量值,不用试验中意义不同。 计算时常用取对数法
在教育研究方面的应用,主要是用来描述学习速度方面的问题。调和平均数作为一种集中量数,在描述速度方面的集中趋势时,优于其他集中量数。 在有关研究学习速度的实验设计中,反应指标一般常取两种形式: 一是工作量固定,记录各被试完成相同工作所用的时间。二是学习时间一定,记录一定时间内各被试完成的工作量。由于反应指标不同,在计算学习速度时也不一样,这是应用调和平均数要特别注意的地方。 学习任务量相同而所用时间不等。这时先要求出单位时间的工作量,并以它为 \(X_i\) 代入调和平均数公式计算,所得结果就是欲求的平均学习速度。
1.2.1 学习任务量相同而所用时间不等

- 解:
假设6名被试者单位时间内完成的作业题数依次为\(X_1,X_2 \cdots X_6\),则 \[X_1 = \frac{10}{0.8},X_2 = \frac{10}{1.0} \cdots X_6=\frac{10}{5}\] 每个被试者完成单位工作所需时间为: \[\frac1X_1=\frac{0.8}{10},\frac1X_2=\frac{1.0}{10}\cdots \frac1X_6=\frac{5}{10}\] 6名被试者完成每到题所需时间总量为: \[\sum \frac1X_i=\sum (\frac1X_1+\frac1X_2 +\cdots+\frac1X_6 ) =\sum(\frac{0.8}{10}+\frac{1.0}{10} +\cdots+\frac{5}{10})=\frac65\] 由\(N=6\)得: \[M_H=\frac1{\frac16 \times \frac65} =5\] 6名被试者平均完成作业的速度是每小时5题
N <- 6
works <- 10
times <- c(0.8,1.0,1.2,1.5,2.5,5.0)
per_hour <- works/times
Mh <- N/sum(1/per_hour) # 5
Mh[1] 5此情形中要求6人平均完成10道题的速度,由于每人学习任务量相同都为10题(可理解为单位工作量扩大10倍),可利用计算平均速度的方式计算调和平均数,即: \[作业平均速度=\frac{总完成题量}{总时间}= \frac {6 \times 10}{0.8+1.0+1.2+1.5+2.5+5.0} =5\] 例2则不同
1.2.2 学习时间相同而工作量不等

- 解:
假设6名被试者单位时间内解题数依次为\(X_1,X_2 \cdots X_6\),则 \[X_1 = \frac{24}{2}=12,X_2 = \frac{20}{2}=10 \cdots X_6=\frac{4}{2}=2\] 每个被试者完成单位工作所需时间为: \[\frac1X_1=\frac{1}{12},\frac1X_2=\frac{1}{10}\cdots \frac1X_6=\frac{1}{2}\]
\[M_H== \frac1{\frac16(\frac{1}{12}+\frac{1}{10} +\cdots+\frac{1}{2})}=\frac{720}{147}=4.9\] 6名被试者平均解题速度是每小时4.9题
[1] 4.897959
