第 11 章 测试特征曲线
在对测试进行评分时,考生对每个项目的回答都会进行二分法评分,正确得 1 分,错误得 0 分,将各项目得分相加得到原始分。对于这种二元计分的测试,原始分数的范围是从 0 到 \(J\)的整数,其中 \(J\) 是测试中的项目数。 若考生再次参加考试,假定他们不记得之前如何回答了这些题目,将会获得一个不同的原始分。现假设一个考生可以多次参加考试并获得各种考试成绩,这些分数会集中在某个平均值附近。在测量理论中,这个值被称为真实分数(true score),其定义取决于特定的测量理论。 在IRT中,采用D.N. Lawley 定义的真实分数。
11.1 真实分数(A True Score)
IRT中,真是分数\(TS_i\)为: \[\mathrm{TS}_{i}=\sum_{j=1}^{J} P_{j}\left(\theta_{i}\right)\] 其中,\(TS_i\)为能力水平为\(\theta_{i}\)的考生的真实分数,\(j\)为项目编号,\(J=1,2...\), \(P_{j}(\theta_{i})\)取决于所采用的ICC模型。
11.2 测试特征曲线(The Test Characteristic Curve)
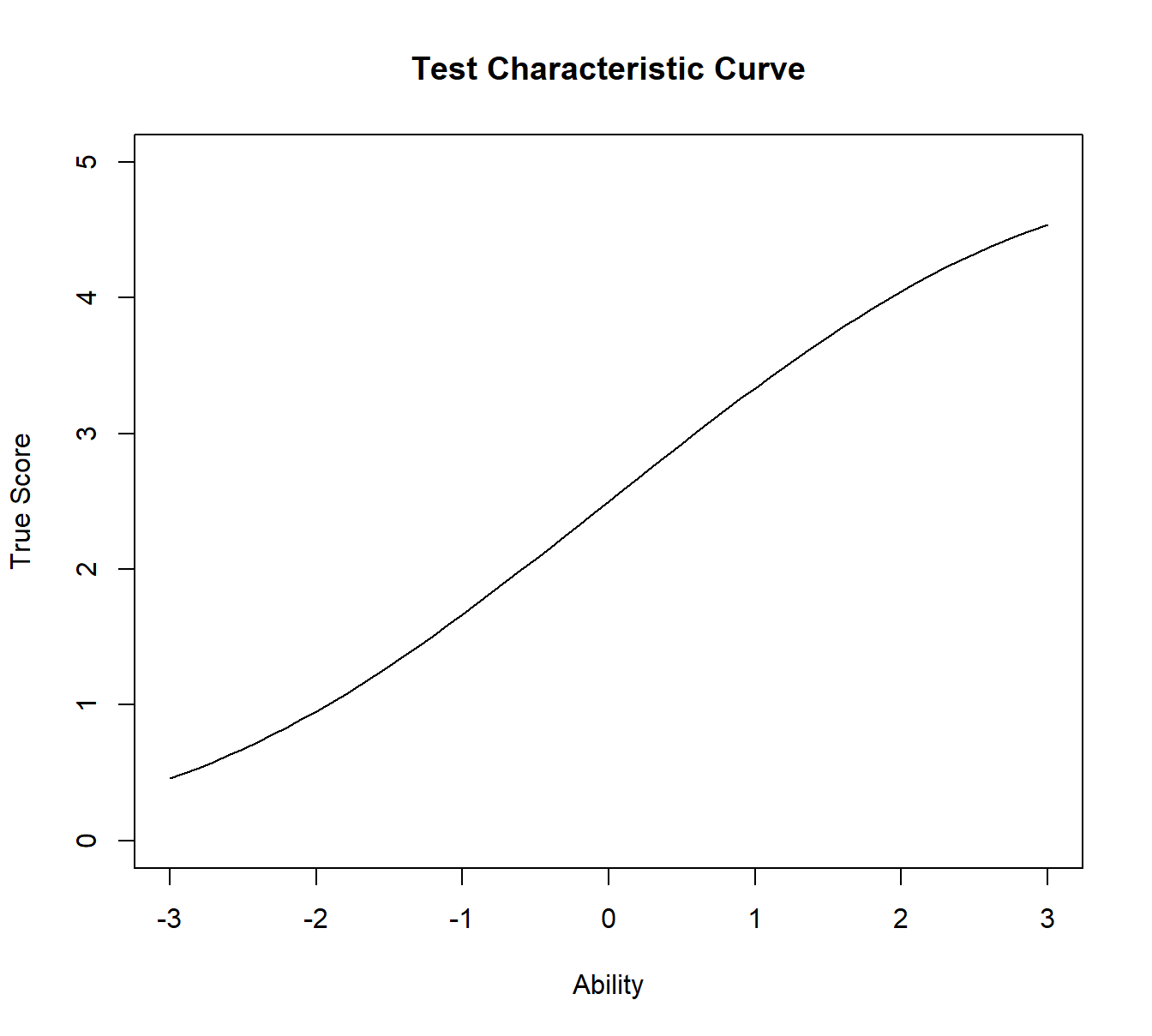
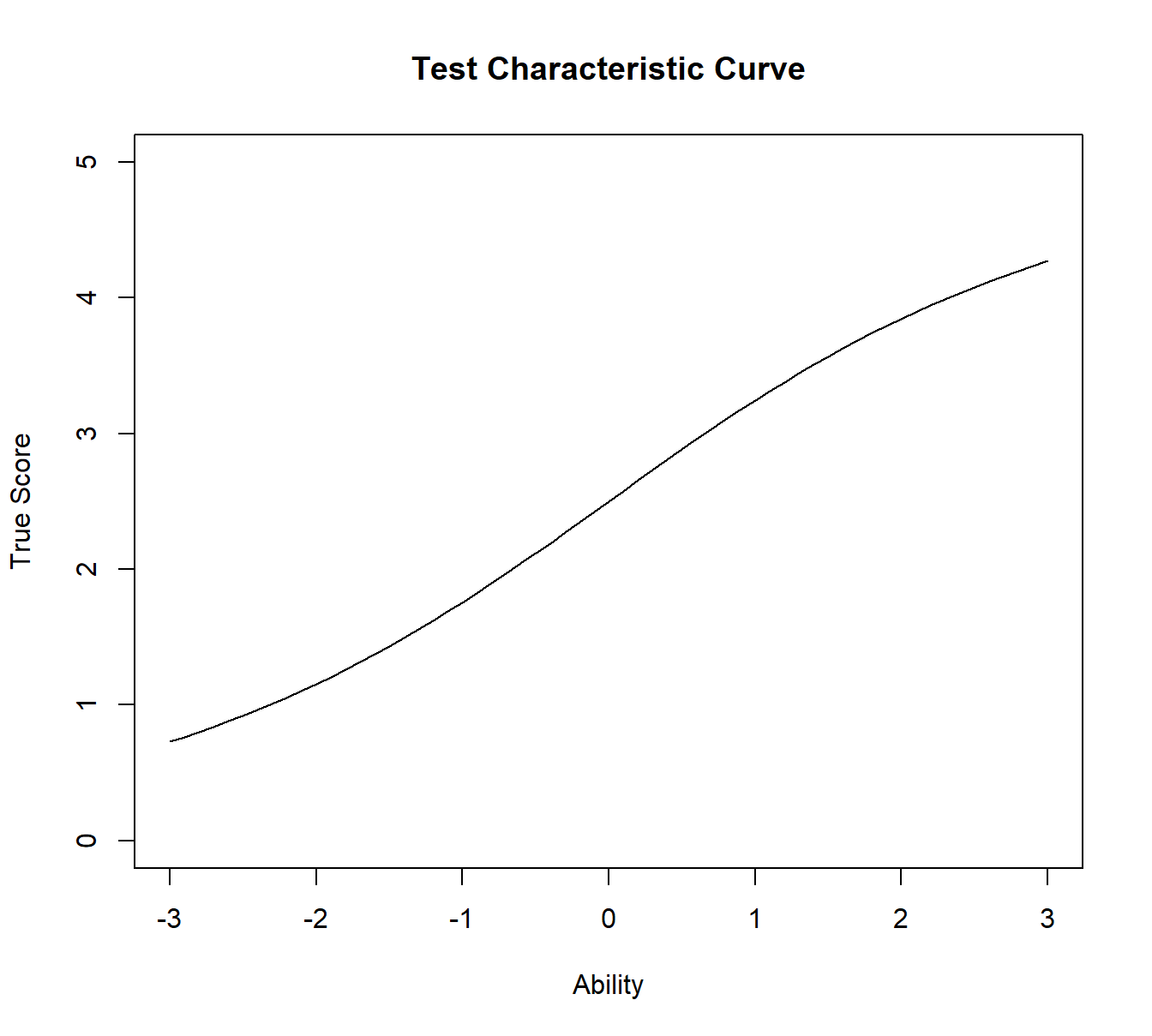
根据真实分数的定义,可以计算能力范围内的任何点的真实分数。以能力值为横坐标,真实分数为纵坐标,即可绘制测试特征曲线。 测验特征曲线表示的是真实分数与能力间的关系。给定任何能力水平,可以通过测试特征曲线找到相应的真实分数。
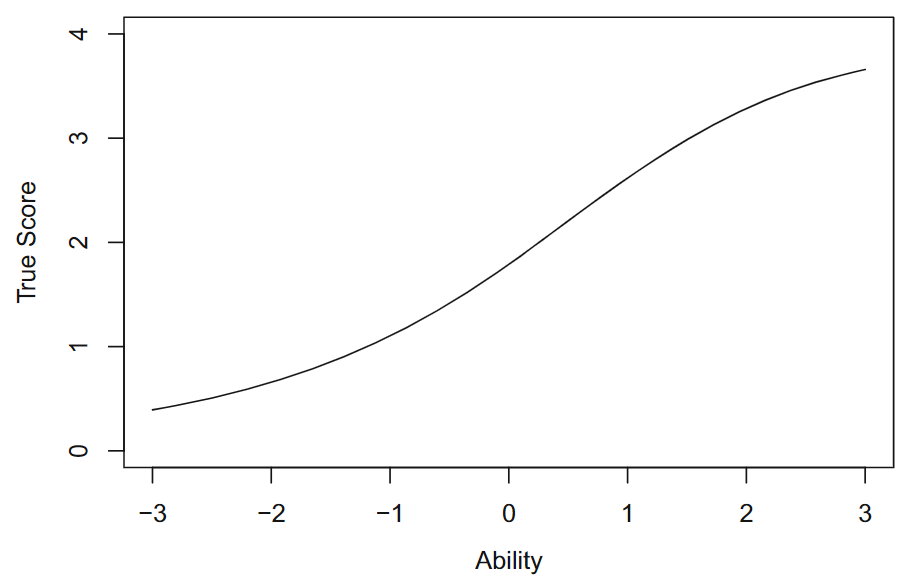
图 11.1: 测试特性曲线(包含4个测试项目:Item1: \(a_{1}=0.5, b_{1}=-1.0\); Item2: \(a_{2}=1.2, b_{2}=0.75\); Item3: \(a_{3}=0.8, b_{3}=0.0\); Item4: \(a_{4}=1.0, b_{4}=0.5\))
在\(J\)个项目的测试中,若每个项目采用Rasch 模型或双参数模型,测试曲线随着能力值趋于负无穷,左尾接近于零,随着能力值接近正无穷,上尾接近测试中的项目数\(J\)。即真实分数为零对应能力值为负无穷大,真实分数为 \(J\) 对应于能力水平为正无穷大。 使用三参数模型时,测验特征曲线的下尾趋近于测验项目的猜测参数之和,即能力非常低的考生可以通过猜测获得大于零的分数。此时曲线上尾仍接近测试中的项目数\(J\)。
在IRT中,测试特征曲线的提供了一种将能力分数转换为真实分数的方法。将能力分数转换为真实分数,便于进行解释。同时,测试特性曲线在等同测试(equating tests)也有重要作用。
测试特征曲线没有明确的公式,因此无明确的参数,画此曲线的方法是使用给定的ICC模型评估测试中所有项目在每个能力水平上正确响应的概率,再将它们在每个能力水平上求和,绘制测试特征曲线。 曲线的解释方式与ICC类似。此外,同ICC一样,测试特征曲线不取决于考生能力值在能力量表上的频率分布,两者都是两个量表之间的函数关系。
11.3 R语言绘制测试特征曲线
tcc <- function(b, a, c) {
J <- length(b)
if (missing(c)) c <- rep(0, J)
if (missing(a)) a <- rep(1, J)
theta <- seq(-3, 3, .1)
ts <- rep(0, length(theta))
for (j in 1:J) {
P <- c[j] + (1 - c[j]) / (1 + exp(-a[j]*(theta-b[j])))
ts <- ts + P
}
plot(theta, ts, type="l", xlim=c(-3,3), ylim=c(0,J),
xlab="Ability", ylab="True Score",
main="Test Characteristic Curve")
}
b <- c(-2.0, -1.0, 0.0, 1.0, 2.0)
a <- c(0.5, 0.75, 1.0, 0.75, 0.5)
c <- c(.2, .2, .2, .2, .2)
tcc(b=b)